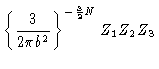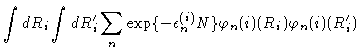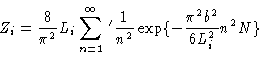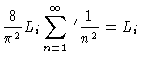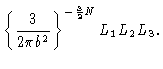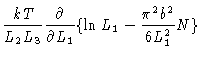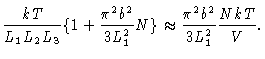Next: Appendix A
Up: The Gaussian chain
Previous: Green's function method
As an example of the use of the Green's function method, we calculate the
pressure exerted by a Gaussian chain on the walls of a confining box .
The potential is zero everywhere inside the box, and infinite everywhere
outside the box. Then
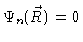 at the walls of the box. Solving Eq. (3.18)
yields
at the walls of the box. Solving Eq. (3.18)
yields
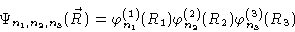 |
(3.21) |
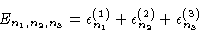 |
(3.22) |
where
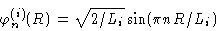 |
(3.23) |
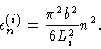 |
(3.24) |
The partition function then reads
| Z |
= |
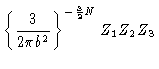 |
(3.25) |
| Zi |
= |
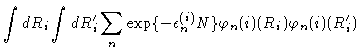 |
(3.26) |
Introducing the eigenfunctions and eigenvalues from Eqs. (3.23) and (3.24) we get
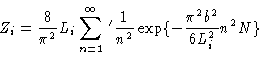 |
(3.27) |
where the prime at the summation sign indicates that only odd n should
occur in the sum.
Now look at two limits
- i.
-
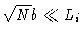
The polymer is much smaller than the box
| Zi |
= |
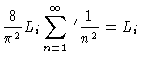 |
(3.28) |
| Z |
= |
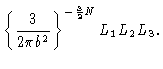 |
(3.29) |
The pressure on wall one is
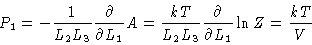 |
(3.30) |
i.e. independent of the wall number, and equal to the ideal gas result.
- ii.
-
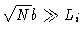
The polymer is very much constrained by the box
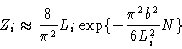 |
(3.31) |
| P1 |
= |
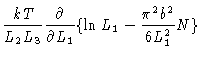 |
(3.32) |
| |
= |
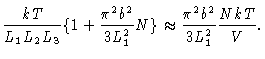 |
(3.33) |
In this case the pressure on the different walls depends on the size of the
box orthogonal to the wall.





Next: Appendix A
Up: The Gaussian chain
Previous: Green's function method
W.J. Briels
![]() at the walls of the box. Solving Eq. (3.18)
yields
at the walls of the box. Solving Eq. (3.18)
yields