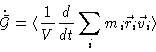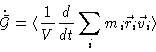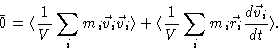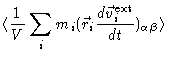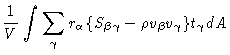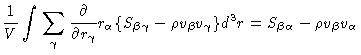Next: B. Suspensions
Up: The virial theorem, and
Previous: The virial theorem, and
We consider a small portion of fluid, small enough for all
macroscopic gradients to be zero, and large enough to represent a
homogeneous phase. Now consider the quantity
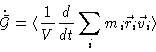 |
(5.57) |
where the average is an ensemble average, or a time average over a time span
long enough to smooth out fluctuations, and short enough to assume that the
macroscopic flow is stationary. The sum is over all particles in our control
volume, i.e. particles leaving the control volume are from that moment on
left out of the sum, and particles entering the control volume will from
that moment on contribute to the sum. Since in this case
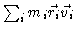 is a bounded quantity, with a well defined average, the
average of its time variation must be zero,
is a bounded quantity, with a well defined average, the
average of its time variation must be zero,
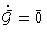 .
.
Evaluating the derivative we obtain
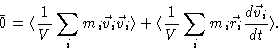 |
(5.58) |
Assuming for simplicity that no body forces are applied, we write
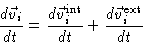 |
(5.59) |
where the first term results from the presence of all particles, except i,
in the control volume, and the second term results from the presence of all
particles outside the control volume.
Since the control volume is assumed to be of macroscopic size, the second
term may be assumed to be concentrated near the boundary of the volume. In
terms of the stress tensor we have
where
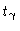 is a component of the outward normal
is a component of the outward normal 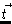 ,
and
,
and 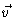 is the average velocity. It has been assumed that gradients in
is the average velocity. It has been assumed that gradients in 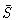 and
and 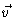 are negligible. Combining everything we get
are negligible. Combining everything we get
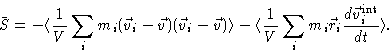 |
(5.61) |
This is the result we were after; it expresses the macroscopic stress tensor
in terms of averages over microscopic quantities.





Next: B. Suspensions
Up: The virial theorem, and
Previous: The virial theorem, and
W.J. Briels