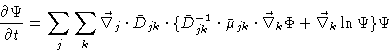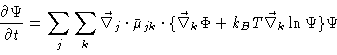Next: Normal coordinates and the
Up: The Zimm chain
Previous: The Zimm chain
One obvious way to improve on the Rouse chain, is by introducing
hydrodynamic interactions between the beads. The chain so defined is
called the Zimm chain . The equations describing hydrodynamic interactions have
been obtained in section 5.4.
Let us now derive the equations of motion of the beads in a Zimm chain. Let
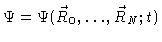 be the probability density of finding
particles
be the probability density of finding
particles
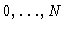 near
near
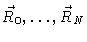 at time t.
The time development of
at time t.
The time development of 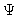 obeys
obeys
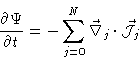 |
(7.1) |
where
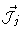 is the flux of particles j. This flux may be
written as
is the flux of particles j. This flux may be
written as
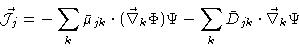 |
(7.2) |
The first term results from the forces
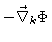 felt by all
the beads. On the Smoluchowski time scale , these forces make the beads move with
constant velocities
felt by all
the beads. On the Smoluchowski time scale , these forces make the beads move with
constant velocities
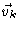 .
This amounts to saying that the forces
.
This amounts to saying that the forces
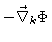 are exactly balanced by the hydrodynamic forces acting on the beads k,
i.e. the forces exerted by the fluid on the beads k are equal to
are exactly balanced by the hydrodynamic forces acting on the beads k,
i.e. the forces exerted by the fluid on the beads k are equal to
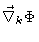 .
Introducing these forces into Eq. (5.54), we
find the systematic part of the velocity of bead j:
.
Introducing these forces into Eq. (5.54), we
find the systematic part of the velocity of bead j:
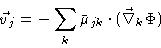 |
(7.3) |
Multiplying this velocity by 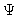 ,
we obtain the systematic part of the
flux of particle j. The second term in Eq. (7.2) stems from
the random displacements of all beads, which result in a flux along the
negative gradient of the probability density.
,
we obtain the systematic part of the
flux of particle j. The second term in Eq. (7.2) stems from
the random displacements of all beads, which result in a flux along the
negative gradient of the probability density.
Combining Eqs. (7.1) and (7.2) we find
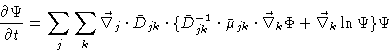 |
(7.4) |
where
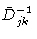 is the inverse of
is the inverse of
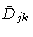 .
In the
stationary state the right hand side must be zero, and
.
In the
stationary state the right hand side must be zero, and
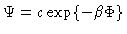 .
From this it follows that
.
From this it follows that
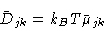 |
(7.5) |
which is a generalization of the Einstein equation .
The equation of motion of the probability density, i.e. the Smoluchowski
equation , now reads
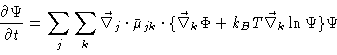 |
(7.6) |
The Langevin equations corresponding to this Smoluchowski equation are
The reader can easily check that these reduce to the equations of motion of
the Rouse chain when hydrodynamic interactions are neglected.
Let us note at this point that for the approximation of the mobility tensor
we make use of
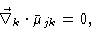 |
(7.9) |
which greatly simplifies Eq. (7.7).





Next: Normal coordinates and the
Up: The Zimm chain
Previous: The Zimm chain
W.J. Briels
![]() be the probability density of finding
particles
be the probability density of finding
particles
![]() near
near
![]() at time t.
The time development of
at time t.
The time development of ![]() obeys
obeys