



Next: Appendix A
Up: The Zimm chain
Previous: Normal coordinates and the
The diffusion coefficient of a Zimm chain can be easily
calculated from Eqs. (7.16) and (7.17). The result
is
| DG |
= |
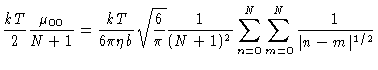 |
(7.19) |
| |
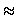 |
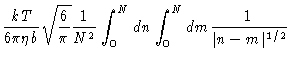 |
(7.20) |
| |
= |
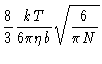 |
(7.21) |
The diffusion coefficient now scales with N-1/2, in agreement with
experiments.
In order to calculate the intrinsic viscosity of a dilute solution of Zimm chains we
go back to Eq. (6.64):
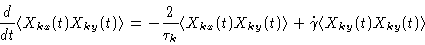 |
(7.22) |
Again we shall approximate
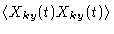 by its
equilibrium value. At the end of this section we shall show that
by its
equilibrium value. At the end of this section we shall show that
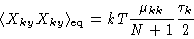 |
(7.23) |
The solution of Eq. (7.22) with this approximation is
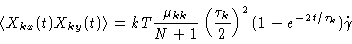 |
(7.24) |
Eqs. (6.53), (6.57) and (7.24) then
yield
![\begin{displaymath}\lbrack \eta ]=\frac{N_{Av}}{M}12\pi \left\{ \frac{(N+1)b^{2}}{12\pi }
\right\} ^{3/2}\sum_{k=1}^{N}\frac{1}{k^{\frac{3}{2}}}
\end{displaymath}](img896.gif) |
(7.25) |
The intrinsic viscosity scales with N3/2, in agreement with experiments.
We finish this section by proving Eq. (7.23). At equilibrium we
have
| 0 |
= |
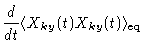 |
(7.26) |
| |
= |
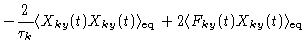 |
(7.27) |
The last term here can be calculated according to
Eq. (7.27), (7.29) and (7.17) yield Eq. (
7.23).




Next: Appendix A
Up: The Zimm chain
Previous: Normal coordinates and the
W.J. Briels
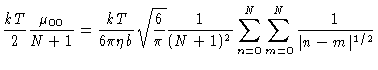
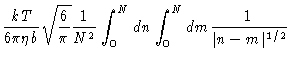
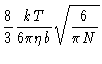
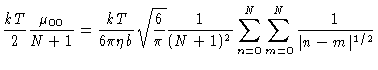
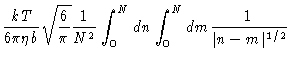
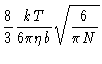
![\begin{displaymath}\lbrack \eta ]=\frac{N_{Av}}{M}12\pi \left\{ \frac{(N+1)b^{2}}{12\pi }
\right\} ^{3/2}\sum_{k=1}^{N}\frac{1}{k^{\frac{3}{2}}}
\end{displaymath}](img896.gif)