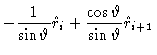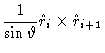



Next: Integral equations for polymer
Up: The Rotational Isomeric State
Previous: Appendix A
From Fig. (1.5) it follows that
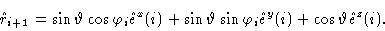 |
(1.50) |
Using this in
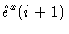 |
= |
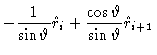 |
(1.51) |
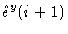 |
= |
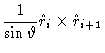 |
(1.52) |
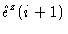 |
= |
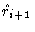 |
(1.53) |
one easily derives
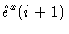 |
= |
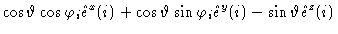 |
(1.54) |
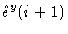 |
= |
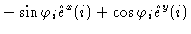 |
(1.55) |
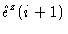 |
= |
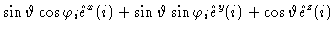 |
(1.56) |
from which the matrix
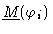 may be read off.
may be read off.
W.J. Briels