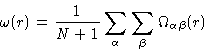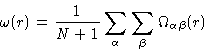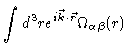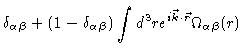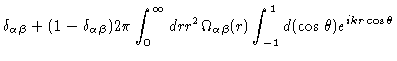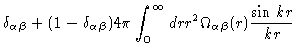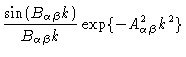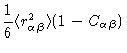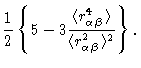



Next: The Gaussian chain
Up: Integral equations for polymer
Previous: Polymer RISM
According to Eq. (2.37)
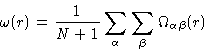 |
(2.39) |
From the discussion at the end of section 2.4 it follows
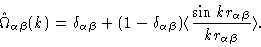 |
(2.40) |
The average may be calculated using the methods of Chapter 1. Usually it is
a good approximation to describe
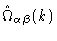 with a
damped sine function
with a
damped sine function
From Fig. (1.3) we conclude that
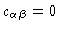 for
for
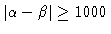 ,
in which case
,
in which case
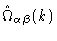 is a simple Gaussian.
is a simple Gaussian.




Next: The Gaussian chain
Up: Integral equations for polymer
Previous: Polymer RISM
W.J. Briels