



Next: The Fokker-Planck equation
Up: Stochastic processes
Previous: Stochastic processes
In this chapter we shall study the basics of the theory of stochastic
processes . This is most easily done in the language of
colloidal suspensions .
Consider a colloidal particle suspended in a liquid. On its path through the
liquid it will continuously collide with the liquid molecules. Because on
average the particle will collide more often on the front side than on the
back side, it will experience a systematic force proportional with its
velocity, and directed opposite to its velocity. Besides this systematic
force the particle will experience a stochastic force
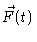 .
The equations of motion then read
.
The equations of motion then read
From hydrodynamics we know that the friction constant 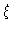 is given by
is given by
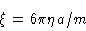 |
(4.3) |
where 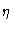 is the viscosity of the solvent and a is the radius of the particle. We
shall derive this and some other results from hydrodynamics in the next
chapter.
is the viscosity of the solvent and a is the radius of the particle. We
shall derive this and some other results from hydrodynamics in the next
chapter.
Solving Eq. (4.2) yields
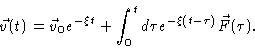 |
(4.4) |
If we want to get some useful information out of this, we have to average
over all possible realizations of
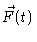 ,
with the initial velocity as
a condition. A useful quantity for example is
,
with the initial velocity as
a condition. A useful quantity for example is
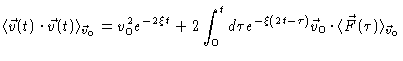 |
| |
|
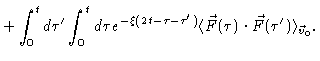 |
(4.5) |
In order to continue we have to make some assumptions about the conditional
averages of the stochastic forces. In view of the chaotic character of the
stochastic forces the following assumptions seem to be appropriate
Here and elsewhere we omit the subscript
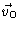 ,
when the quantity of
interest turns out to be independent of
,
when the quantity of
interest turns out to be independent of
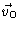 .
Using Eqs. (4.6) and (4.7) in Eq. (4.5) we get
.
Using Eqs. (4.6) and (4.7) in Eq. (4.5) we get
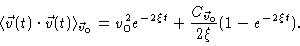 |
(4.8) |
For large t this should be equal to 3kT/m, from which it follows that
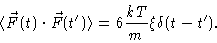 |
(4.9) |
This result is called the fluctuation-dissipation theorem .
Integrating Eq. (4.4) we get
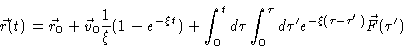 |
(4.10) |
from which we calculate the mean square displacement
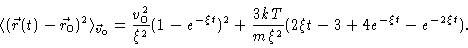 |
(4.11) |
For very large t this becomes
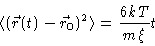 |
(4.12) |
from which we get the Einstein relation
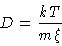 |
(4.13) |
where we have used
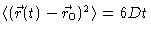 .
.




Next: The Fokker-Planck equation
Up: Stochastic processes
Previous: Stochastic processes
W.J. Briels
![]() .
The equations of motion then read
.
The equations of motion then read