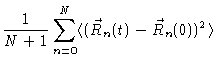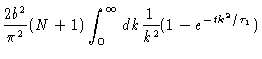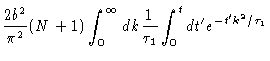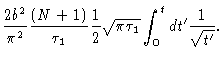Next: Viscosity of a dilute
Up: The Rouse chain
Previous: Correlation of the end-to-end
In this section we study the mean square displacements of the individual monomers. Using
Eq. (6.24) and the fact that different modes are not
correlated, we get
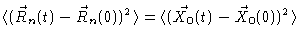 |
| |
|
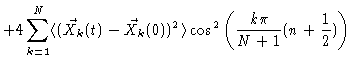 |
(6.43) |
Introducing Eq. (6.38) we get
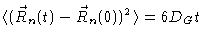 |
| |
|
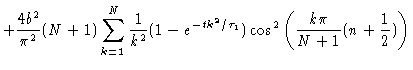 |
(6.44) |
where we have used Eqs. (6.30) and (6.31) to
calculate the first term, and Eqs. (6.39) and (6.40
) for the second term.
There are two different limits to Eq. (6.44). First, when tis very large, i.e.
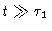 ,
the first term will dominate, yielding
,
the first term will dominate, yielding
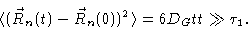 |
(6.45) |
This is consistent with the fact that the polymer as a whole diffuses with
diffusion constant DG.
Secondly, suppose
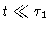 .
Then the sum in Eq. (6.44)
will dominate. Averaging over all monomers, and replacing the sum over kby an integral we get
.
Then the sum in Eq. (6.44)
will dominate. Averaging over all monomers, and replacing the sum over kby an integral we get
Performing the final integral we get
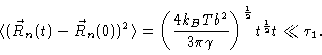 |
(6.47) |
So, at short times the mean square displacement of a typical monomer goes
like the square root of t.





Next: Viscosity of a dilute
Up: The Rouse chain
Previous: Correlation of the end-to-end
W.J. Briels
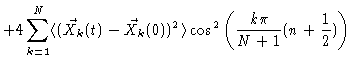
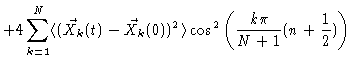
![]() ,
the first term will dominate, yielding
,
the first term will dominate, yielding
![]() .
Then the sum in Eq. (6.44)
will dominate. Averaging over all monomers, and replacing the sum over kby an integral we get
.
Then the sum in Eq. (6.44)
will dominate. Averaging over all monomers, and replacing the sum over kby an integral we get