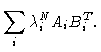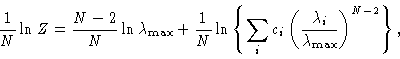Next: Some probabilities
Up: The Rotational Isomeric State
Previous: The model
The RIS model can be treated in considerable detail. As a first step we
calculate the partition function
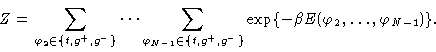 |
(1.3) |
Introducing the energy (1.2) and using a short hand notation for
the summations we get
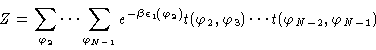 |
(1.4) |
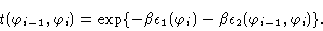 |
(1.5) |
We recognize a sequence of matrix products in Eq. (1.4), which
makes it possible to write
![\begin{displaymath}Z=\sum_{\varphi _{2}}\sum_{\varphi _{N-1}}e^{-\beta \epsilon _{1}(\varphi
_{2})}[T^{N-3}]_{\varphi _{2},\varphi _{N-1}}
\end{displaymath}](img24.gif) |
(1.6) |
T is a matrix with elements
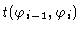 .
In the case
of polyethylene it is given by
.
In the case
of polyethylene it is given by
| |
|
 |
|
| |
|
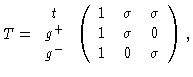 |
(1.7) |
where
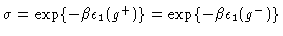 and
and
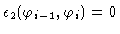 except for
except for
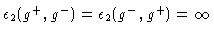 .
The zero of
energy has been chosen such that
.
The zero of
energy has been chosen such that
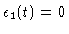 .
.
Eq. (1.6) may also be written as
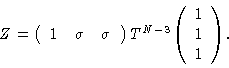 |
(1.8) |
Moreover, using
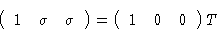 |
(1.9) |
we may write
with
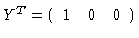 and
and
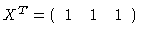 .
.
It is useful to decompose the matrix T in terms of its eigenvectors:
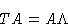 |
(1.11) |
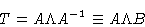 |
(1.12) |
where 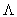 is the diagonal matrix containing the eigenvalues of T.
For notational convenience we have introduced
B = A-1.
is the diagonal matrix containing the eigenvalues of T.
For notational convenience we have introduced
B = A-1.
Eq. (1.12) may be written like
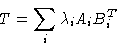 |
(1.13) |
where the Ai are the columns of A and the BiT the rows of B.
Then
| TN |
= |
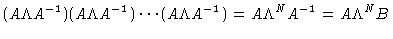 |
|
| TN |
= |
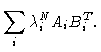 |
(1.14) |
The partition function then reads
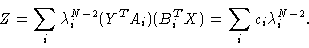 |
(1.15) |
In practice we are usually interested in the free energy per monomer
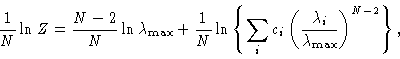 |
(1.16) |
where
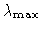 is the largest eigenvalue of T. In the
limit of N going to infinity the second term goes to zero
is the largest eigenvalue of T. In the
limit of N going to infinity the second term goes to zero
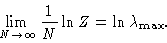 |
(1.17) |
In the case of matrix (1.7) one easily calculates the
eigenvectors. From
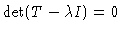 one gets
one gets
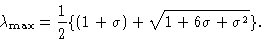 |
(1.18) |





Next: Some probabilities
Up: The Rotational Isomeric State
Previous: The model
W.J. Briels
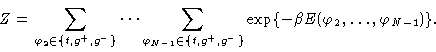
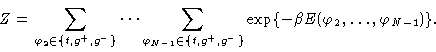
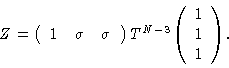
![]() and
and
![]() .
.