



Next: The radius of gyration
Up: The Rotational Isomeric State
Previous: Some probabilities
A rough measure of the average size of the polymer is given by the mean
square end-to-end vector , which we shall calculate in this section. Related
properties are the radius of gyration , and the persistence length . Both of them may be calculated using methods
similar to the ones in this section.
The end-to-end vector is given by
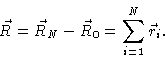 |
(1.27) |
The mean square then reads
Again assuming the chain is infinitely long, we may put
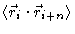 independent on i. Then
independent on i. Then
where (N-n) is the number of times the distance n may occur along the
chain.
We now set forth to calculate
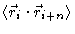 .
In order to do so we need to calculate the scalar product
.
In order to do so we need to calculate the scalar product
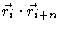 as a function of the angles
as a function of the angles
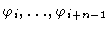 .
To this end we associate with every monomer i a
Cartesian coordinate system
.
To this end we associate with every monomer i a
Cartesian coordinate system
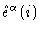 .
Every vector
.
Every vector 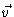 may then be expanded like
may then be expanded like
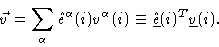 |
(1.30) |
The precise definition of the local coordinate system is given in Appendix
A. Here we only mention that
A particular example of Eq. (1.30) is
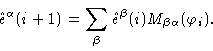 |
(1.32) |
The matrix
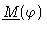 is calculated in Appendix B.
is calculated in Appendix B.
The scalar product
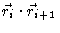 now reads
now reads
and in general
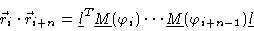 |
(1.34) |
from which we get
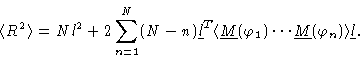 |
(1.35) |
We finally calculate the remaining average using the methods of the last
section
where again we have omitted the subscript ''max''. We may write this in a
concise form like
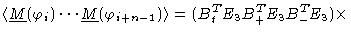 |
| |
|
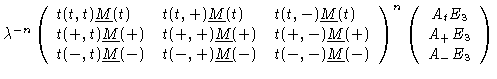 |
(1.37) |
where E3 is the 3-d unit matrix. In terms of direct products of matrices
this reads
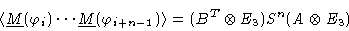 |
(1.38) |
Introducing everything into Eq. (1.35) we get
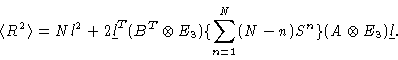 |
(1.40) |
For infinitely long chains we can analytically sum, obtaining
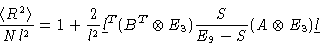 |
(1.41) |
where E9 is the 9-d unit matrix. In this derivation of Eq. (1.41) we have made use of
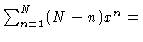
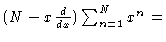
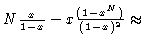
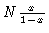 for large N.
for large N.
Similar equations, but much more complicated, may be derived for
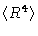 .
For these and other equations we refer to P.J. Flory,
Statistical Mechanics of Chain Molecules .
.
For these and other equations we refer to P.J. Flory,
Statistical Mechanics of Chain Molecules .




Next: The radius of gyration
Up: The Rotational Isomeric State
Previous: Some probabilities
W.J. Briels
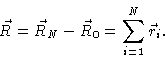
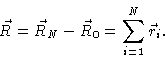
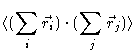
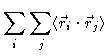
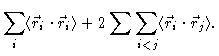
![]() .
In order to do so we need to calculate the scalar product
.
In order to do so we need to calculate the scalar product
![]() as a function of the angles
as a function of the angles
![]() .
To this end we associate with every monomer i a
Cartesian coordinate system
.
To this end we associate with every monomer i a
Cartesian coordinate system
![]() .
Every vector
.
Every vector ![]() may then be expanded like
may then be expanded like
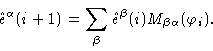
![]() now reads
now reads
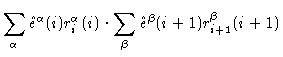
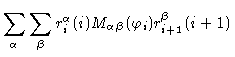
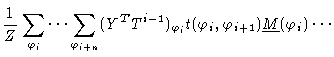
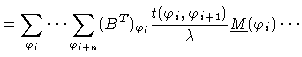
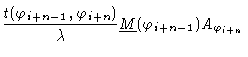
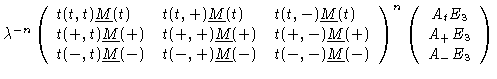
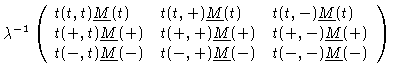
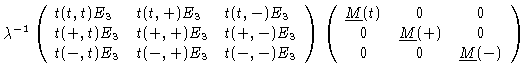
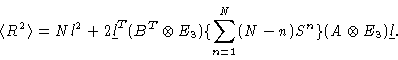
![]() .
For these and other equations we refer to P.J. Flory,
Statistical Mechanics of Chain Molecules .
.
For these and other equations we refer to P.J. Flory,
Statistical Mechanics of Chain Molecules .