Research Highlights

protein aggregation

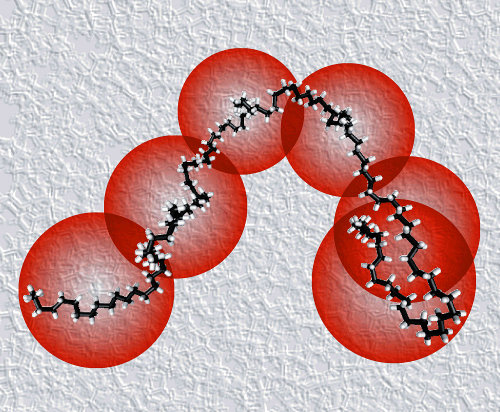
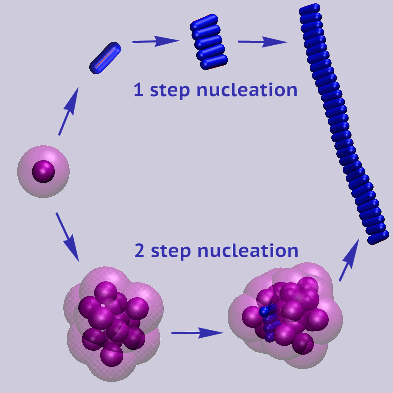
We developed a highly coarse grained model to study the aggrgation of α-synuclein, the protein associated with Parkinson's disease [1], into ordered structures. We represent proteins as soft bodies of various shapes with attractive patches on their surfaces. To simulate dynamics we have implemented a Brownian Dynamics algorithm for the translational and rotational motion [2]. Simulation results show the formation of oligomers and fibrils by a direct nucleation-and-growth mechanism, by two-step-nucleation through the conversion of an oligomer into a fiber or vice versa, and by fibril-enhanced cinversion of oligomers into fibrils [1].

self-assembly

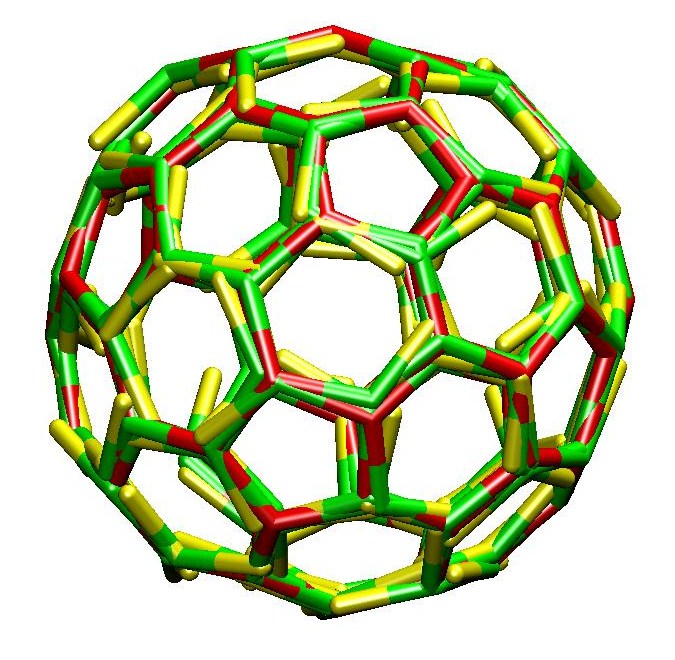
We have presented the first simulations of the self-assembly of three-legged clathrin proteins into polyhedral cages. In living cells clathrin lattices grow next to the cell membrane, thereby wrapping the membrane around any external cargo the cell wants to internalize (endocytosis). The simulations reveal that the key to cage formation lies not with clathrin's characteristic shape, but rather requires leg-leg interactions with a directionality  [3, 4, 5]. We also made the first estimate of the binding energy [6]. Click here for a movie (20MB).

free energies

Intermediate states of reactions are conveniently studied in molecular dynamics simulations by suppressing motion along the reaction coordinate. We introduced the exact relation between the constraint force and the free energy profile [7]. While the remaining internal coordinates are clearly irrelevant, we were the first to show that they are not required in the calculation either [8]. As an example, these methods enabled us to determine the free energy profile of pore formation in lipid membranes [9,10], by introducing a novel reaction coordinate based on the local particle density.

liquid crystals

We have pioneered event-driven Brownian dynamics [11], in order to study the flow behaviour of liquid-crystalline suspensions of elongated hard rods. The simulations clearly show the collective tumbling motion of the rods under shear flow, in good agreement with the motion of the director in experiments [12]. The simulations reveal that the rods tumble at all shear rates, and explain why measured directors stops tumbling at a critical shear rate [13]. Click here for a movie (29MB).

hydrodynamics

We have merged molecular dynamics with stochastic rotation dynamics [14] to capture the combined effects of Brownian and hydrodynamic forces in colloidal suspensions. This enabled us to study, for the first time, the sedimentation of hard spheres [15] and of attractive colloidal particles [16], highlighting the importance of hydrodynamic backflow and clustering on the mean sedimentation velocity. These movies show the difference between colloids sedimenting with (6MB) and without (6MB) hydrodynamics. 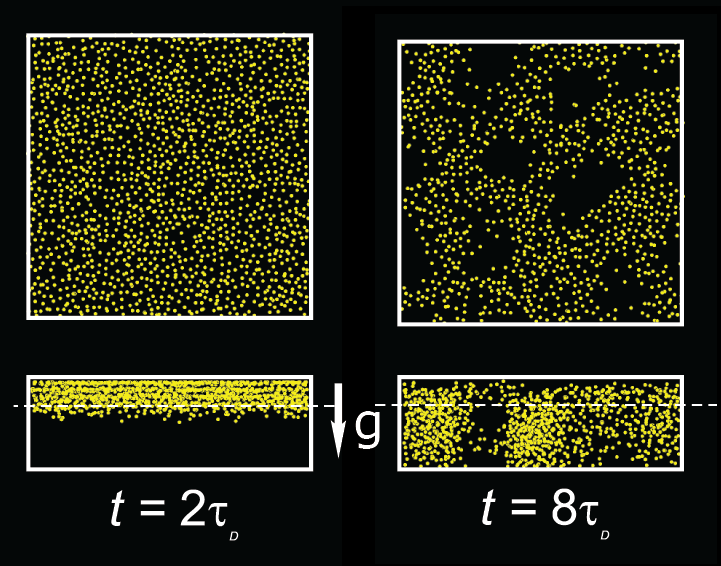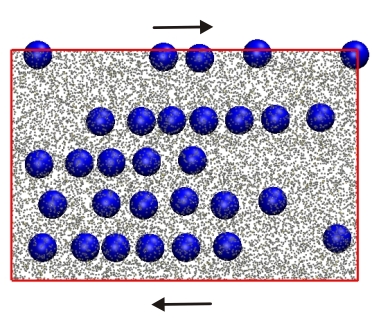Sedimentation in a planar slit gives rise to pattern formation, shown on the right in side view (bottom) and in horizontal cross section (top, at height of dashed line).

visco-elastic fluids

We have developed Responsive Particle Dynamics (RaPiD) to simulate soft matter at the mesoscopic level, by modeling complex molecules as single particles [17]. The crux of the method is that every particle pair is endowed with an internal coordinate describing the evolution of the pair interaction, thereby naturally introducing the transient forces responsible for the memory effect of viscoelastic fluids [18]. RaPiD has succesfully been applied to study shear-banding resins, shear-fracturing telechelics [19], and shear-induced alignment (picture) of colloids dissolved in worm-like micelles, among others. Click here for a movie (35MB).

polymer dynamics

Atomistic molecular dynamics simulations of polymer melts become exceedingly slow for chains beyond ~100 carbons. Longer chains require coarse-grained models, combining ~20 carbons into a single particle, but the effective interactions between these beads are so soft that the chains lose their most important feature: their uncrossibility. We have developed twentanglement to preserve uncrossibility in coarse-grained simulations [20], thereby recovering excellent scaling laws (diffusion with power -2, viscosity with power 3.5) for linear polyethylene upto 1000 carbons [21].

selected publications