




Next: Polymer RISM
Up: Integral equations for polymer
Previous: The Ornstein-Zernike equation and
We shall now generalize the results of the previous section to molecular
liquids . We view the liquid at first as being a mixture of
atomic liquids, containing as many components as there are atoms in the
molecule. Eq. (2.3) then simply generalizes to
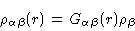 |
(2.23) |
where
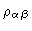 is the density of
is the density of 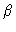 -atoms at a distance
r from a given
-atoms at a distance
r from a given 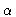 -atom. We use capital
-atom. We use capital
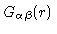 here
for reasons to become clear in a minute. Defining
here
for reasons to become clear in a minute. Defining
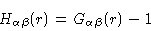 |
(2.24) |
the OZ equation becomes
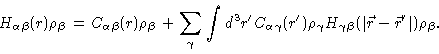 |
(2.25) |
Dividing by
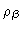 and Fourier transforming we get in matrix
notation
and Fourier transforming we get in matrix
notation
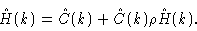 |
(2.26) |
Here 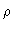 is the diagonal matrix with elements
is the diagonal matrix with elements
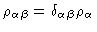 .
The transition to
.
The transition to 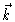 -space
is only for reason of simpler notation.
-space
is only for reason of simpler notation.
We of course know that the correlations between the atoms are partly due to
the fact that they form molecules. Therefore we write
where
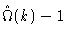 stems from the intramolecular correlations and
stems from the intramolecular correlations and
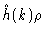 from the intermolecular correlations .
from the intermolecular correlations .
In the ideal gas limit we may approximate
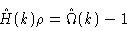 |
(2.28) |
which, when introduced into the OZ equation (2.26) yields
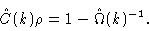 |
(2.29) |
We therefore write in general
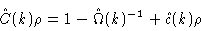 |
(2.30) |
where
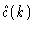 is called the intermolecular part of the direct
correlation function matrix. Introducing Eqs. (2.27) and (
2.30) into the OZ equation we get after some algebra
is called the intermolecular part of the direct
correlation function matrix. Introducing Eqs. (2.27) and (
2.30) into the OZ equation we get after some algebra
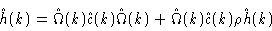 |
(2.31) |
where we have used the fact that 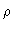 and
and
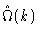 commute. For
pure molecular liquids this follows from the fact that
commute. For
pure molecular liquids this follows from the fact that 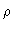 is equal to
the molecular density times the unit matrix. A proof for molecular mixtures
is a little bit more involved. Once we know the intramolecular correlation
is equal to
the molecular density times the unit matrix. A proof for molecular mixtures
is a little bit more involved. Once we know the intramolecular correlation
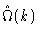 we may calculate the intermolecular correlation from Eq. (
2.31) by using one of the closure relations
we may calculate the intermolecular correlation from Eq. (
2.31) by using one of the closure relations
which we simply try in analogy with similar calculations on simple liquids.
Of course this may turn out to be a very crude approximation. Experience so
far shows that it works well as long as one is interested in describing the
local structure in the liquid. For very small values of the wavevector k,
or equivalently at large values of r problems occur which make
thermodynamic predictions unreliable.
We end this section with some remarks about the intramolecular correlation function. We Fouriertransform
Eq. (2.27), and next add
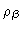 to each of its
elements, obtaining
to each of its
elements, obtaining
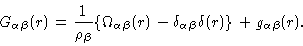 |
(2.34) |
Here
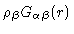 is the density of
is the density of 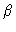 -atoms
at a distance r from an
-atoms
at a distance r from an 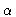 -atom; when
-atom; when
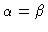 the atom at
the origin does, by definition, not contribute to the density.
the atom at
the origin does, by definition, not contribute to the density.
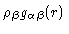 is defined in exactly the same way, with the proviso
that the
is defined in exactly the same way, with the proviso
that the 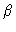 -atom should be on another molecule than the
-atom should be on another molecule than the 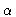 -atom. Using these definitions we see that
-atom. Using these definitions we see that
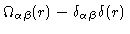 is the density of
is the density of 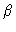 -atoms at
a distance r from an
-atoms at
a distance r from an 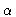 -atom, where
-atom, where 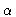 and
and 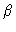 should
be on the same molecule, and where, in the case
should
be on the same molecule, and where, in the case
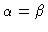 ,
the atom
at the origin does not contribute to the density. So finally we conclude
that
,
the atom
at the origin does not contribute to the density. So finally we conclude
that
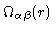 is the density of
is the density of 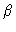 -atoms at a
distance r from an
-atoms at a
distance r from an 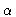 -atom, with the
-atom, with the 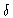 -peak included when
-peak included when
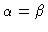 .
In the latter case
.
In the latter case
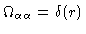 ,
because the total number of
,
because the total number of 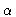 -atoms in each molecule equals one.
-atoms in each molecule equals one.





Next: Polymer RISM
Up: Integral equations for polymer
Previous: The Ornstein-Zernike equation and
W.J. Briels
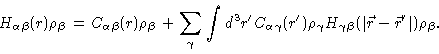
![]() to each of its
elements, obtaining
to each of its
elements, obtaining