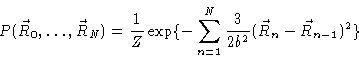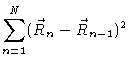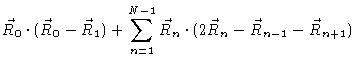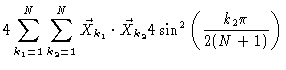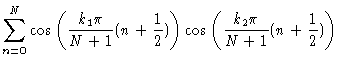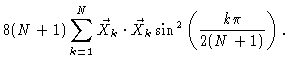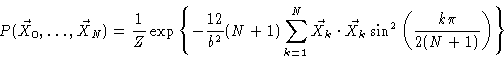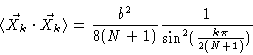



Next: The Zimm chain
Up: The Rouse chain
Previous: Summary
In this appendix we calculate the equilibrium expectation value of Xk2.
In Cartesian coordinates the statistical weight of some configuration
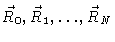 is given by
is given by
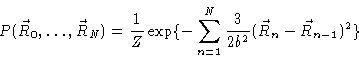 |
(6.77) |
Since the transformation to normal coordinates is a linear transformation
from one set of orthogonal coordinates to another, the corresponding
Jacobian is simply a constant. The argument of the exponential may be
written as
The statistical weight therefore reads
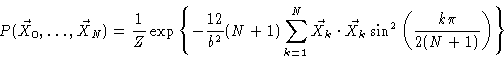 |
(6.79) |
Since this is a simple product of independent Gaussians, all kinds of
expectation values may easily be calculated, like for example
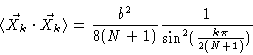 |
(6.80) |




Next: The Zimm chain
Up: The Rouse chain
Previous: Summary
W.J. Briels
![]() is given by
is given by