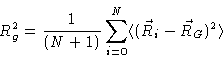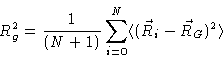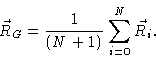



Next: Some results for polyethylene
Up: The Rotational Isomeric State
Previous: The mean square end-to-end
An alternative measure of the size of a polymer chain is provided by its
radius of gyration ,
which may be measured by light scattering
experiments . It is defined by
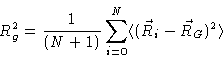 |
(1.42) |
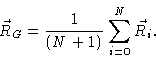 |
(1.43) |
It measures the average squared distance to the centre of gravity
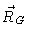 .
.
A little manipulation yields
It is clear that expressions for Rg can easily be obtained using methods
similar to the ones of the previous section.




Next: Some results for polyethylene
Up: The Rotational Isomeric State
Previous: The mean square end-to-end
W.J. Briels