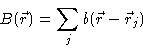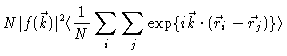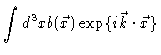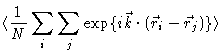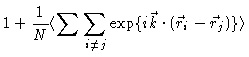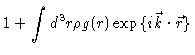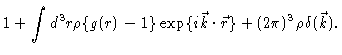Next: The Ornstein-Zernike equation and
Up: Integral equations for polymer
Previous: Flory's hypothesis
Consider a simple atomic liquid or colloidal suspension . The average density 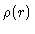 at a distance r of a given particle is defined to be
at a distance r of a given particle is defined to be 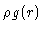 ,
i.e.
,
i.e.
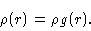 |
(2.3) |
Here 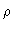 is the average density in the fluid. Notice that
is the average density in the fluid. Notice that 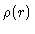 is
a conditional density; it is the density at
is
a conditional density; it is the density at 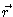 ,
given a particle is present in the origin. A qualitative picture
of g(r) is given in Fig. (2.1); it is called the radial
distribution function .
,
given a particle is present in the origin. A qualitative picture
of g(r) is given in Fig. (2.1); it is called the radial
distribution function .
It is clear that g(r) should go to 1 for large r. At very short rthe radial distribution function must be zero, because two particles cannot
occupy the same space. Outside the van der Waals diameter, there is a peak
because the remaining N-1 particles try to diffuse into the region
occupied by the one at the origin. The surplus of particles in the first
peak causes a lack of particles a little bit further on, explaining the
minimum of g(r) around 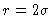 .
.
Figure 2.1:
Radial distribution function.
|
|
Radial distribution functions may be measured by means of scattering
experiments, for example by means of X-ray or neutron scattering in the case of atomic liquids, or by means of
SAXS, SANS or light scattering in the case of colloidal suspensions. Generally the
sample produces a scattering amplitude
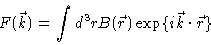 |
(2.4) |
at the detector. Here
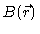 is the scattering power at position
is the scattering power at position 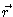 ,
and
,
and 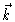 is defined by
is defined by
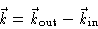 |
(2.5) |
where
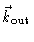 and
and
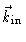 are the
wavevectors of the outgoing and incoming wave respectively. The
measured intensity is proportional to
are the
wavevectors of the outgoing and incoming wave respectively. The
measured intensity is proportional to
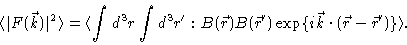 |
(2.6) |
Writing the scattering power like
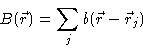 |
(2.7) |
we find after some algebra
The important quantity for us is
The  -function only gives a contribution at
-function only gives a contribution at
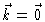 ,
i.e. to the forward scattering. At all other k-values one measures the
scattering factor
,
i.e. to the forward scattering. At all other k-values one measures the
scattering factor
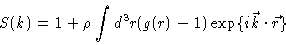 |
(2.11) |
i.e. essentially the Fourier transform of the total correlation function
h(r)=g(r)-1.
Once we have determined the radial distribution function we may calculate
several quantities of interest, like
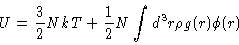 |
(2.12) |
 |
(2.13) |
where 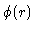 is the interaction potential between two particles in the system, and Uand P are the thermodynamic energy and pressure respectively. Another important relation is the
compressibility equation
is the interaction potential between two particles in the system, and Uand P are the thermodynamic energy and pressure respectively. Another important relation is the
compressibility equation
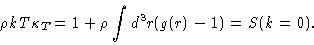 |
(2.14) |
For more information we refer to any book on liquid state theory, like for
example J. -P. Hansen and I. R. McDonald , Theory of simple liquids.





Next: The Ornstein-Zernike equation and
Up: Integral equations for polymer
Previous: Flory's hypothesis
W.J. Briels
![]() at a distance r of a given particle is defined to be
at a distance r of a given particle is defined to be ![]() ,
i.e.
,
i.e.
![]() .
.