As we have stressed at the beginning of the
previous section, the surplus of density
![]() may be
regarded as being the convolution of a short range function and
may be
regarded as being the convolution of a short range function and ![]() itself. We formalize this by introducing the direct correlation function c(r) according to
itself. We formalize this by introducing the direct correlation function c(r) according to
A simple relation exists between S(k) and the Fourier transform
![]() of c(r). Fourier transforming Eq. (2.15) we get
of c(r). Fourier transforming Eq. (2.15) we get
| = | (2.16) | ||
| S(k) | = | 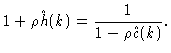 |
(2.17) |
| = | 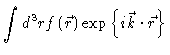 |
(2.18) | |
| = | 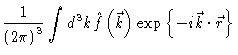 |
(2.19) |
We have introduced the direct correlation function such that it is a short
range function. Writing
| (2.20) |
| c(r)=g(r)-y(r). | (2.21) |
For a first principles derivation of the Percus-Yevick equation we refer to
the literature mentioned above. Using a slightly different approximation
than the one producing the PY closure, one may also derive
| (2.22) |
Here we restrict ourselves to mentioning that both equations have been very successful in predicting correlation functions, the PY equation being the more successful one in the case of hard spheres , and the HNC being the more successful one in the case of Lennard-Jones atoms.