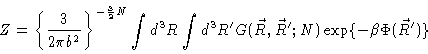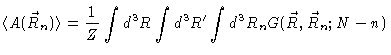Next: One Gaussian chain in
Up: The Gaussian chain
Previous: The Gaussian chain
In this section we shall investigate the Gaussian chain at a level where the distance between two consecutive
beads may be considered to be small.
Suppose we study a Gaussian chain in an external field with potential
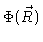 .
The distribution in configuration space then reads
.
The distribution in configuration space then reads
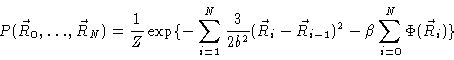 |
(3.12) |
where Z is a normalizing constant. In many cases we are interested in
properties depending on the position vectors of only a few beads along the
chain. It will turn out to be useful then to introduce the Green's function
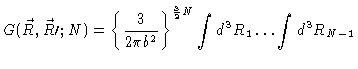 |
| |
|
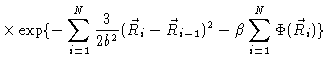 |
(3.13) |
where
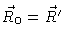 and
and
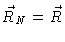 .
Notice
that the Green's function is not normalized. One easily verifies however
.
Notice
that the Green's function is not normalized. One easily verifies however
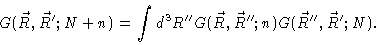 |
(3.14) |
This equation is called the Chapman-Kolmogorov equation . For this equation to hold true, it is
essential that the second summation in the exponent in Eq. (3.13) starts at i=1, and not at i=0 as in Eq. (3.12).
Now we shall treat N like a continuous variable. In Appendix C we shall
prove that
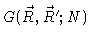 is the solution of
is the solution of
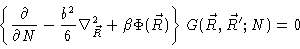 |
(3.15) |
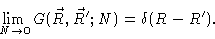 |
(3.16) |
Accepting this for the moment we may immediately write down the formal
solution
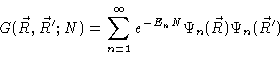 |
(3.17) |
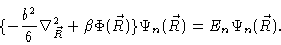 |
(3.18) |
One easily checks this by introducing Eq. (3.17) into Eq. (
3.15) and using Eq. (3.18). Eq. (3.16) is nothing but the closure equation of the complete set of
functions.
Knowing
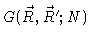 makes it possible to calculate all
kinds of averages:
makes it possible to calculate all
kinds of averages:
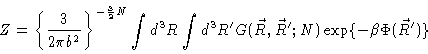 |
(3.19) |
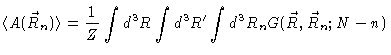 |
| |
|
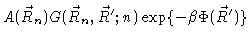 |
(3.20) |
etc.





Next: One Gaussian chain in
Up: The Gaussian chain
Previous: The Gaussian chain
W.J. Briels
![]() .
The distribution in configuration space then reads
.
The distribution in configuration space then reads
![]() is the solution of
is the solution of
![]() makes it possible to calculate all
kinds of averages:
makes it possible to calculate all
kinds of averages: