




Next: Appendix A
Up: Stochastic processes
Previous: The Smoluchowski time scale
We shall now derive the equivalent of the Fokker-Planck equation, but this
time applicable at the Smoluchowski timescale.
Suppose we are given a distribution
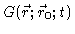 of particles
which were at position
of particles
which were at position
 at time t=0. We assume that the
particles are at every instant of time in thermal equilibrium with respect
to their velocities. A flux will exist, given by
at time t=0. We assume that the
particles are at every instant of time in thermal equilibrium with respect
to their velocities. A flux will exist, given by
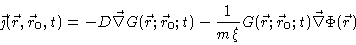 |
(4.29) |
where D is the diffusion constant , occurring in
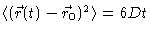 ,
and
,
and 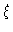 is the friction
coefficient on the Smoluchowski timescale. At equilibrium,
the flux must be zero and the distribution be equal to
is the friction
coefficient on the Smoluchowski timescale. At equilibrium,
the flux must be zero and the distribution be equal to
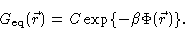 |
(4.30) |
Using this in Eq. (4.29) while setting
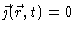 ,
leads to the Einstein equation (4.13).
,
leads to the Einstein equation (4.13).
Introducing Eq. (4.29) into the equation of particle
conservation
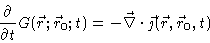 |
(4.31) |
we get the Smoluchowski equation
In the remaining part of this section we shall substantiate the above
derivation. First we define the particle distribution on the Smoluchowski
timescale by
Averaging the Fokker-Planck equation over the initial velocities and integrating
over  ,
we find the continuity equation Eq. (4.31), with
,
we find the continuity equation Eq. (4.31), with
where the second step serves to define the velocity
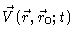 at time t at position
at time t at position 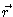 ,
given that the particle was
originally at
,
given that the particle was
originally at
 .
.
We next derive an equation describing the time development of the velocity
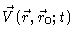 .
To this end we multiply the Fokker-Planck
equation by
.
To this end we multiply the Fokker-Planck
equation by 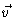 ,
average over the initial velocities, and integrate
over
,
average over the initial velocities, and integrate
over 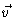 ,
obtaining
,
obtaining
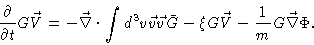 |
(4.37) |
Using the continuity equation and rearranging we find
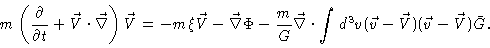 |
(4.38) |
In a strongly damped system the integral on the right hand side yields the
velocity fluctuation at position 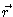 ,
multiplied by the probability to
find the particle at position
,
multiplied by the probability to
find the particle at position 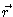 ,
which is
GkT1/m. On the
left hand side we recognize the acceleration of the particle at
,
which is
GkT1/m. On the
left hand side we recognize the acceleration of the particle at 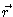 (see section 5.1). Eq. (4.38) may then be written as
(see section 5.1). Eq. (4.38) may then be written as
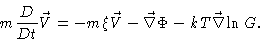 |
(4.39) |
In a strongly damped system the average particle velocity is almost
constant. We therefore put the left hand side of Eq. (4.39)
equal to zero and solve for 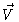 .
Introducing the result into Eq. (4.36) we find the flux Eq. (4.29) and next the
Smoluchowski equation. In Eq. (4.39)
.
Introducing the result into Eq. (4.36) we find the flux Eq. (4.29) and next the
Smoluchowski equation. In Eq. (4.39)
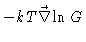 is
called the Brownian force.
is
called the Brownian force.
In appendix B we shall present an alternative derivation of the Smoluchowski
equation. In appendix C we will demonstrate that the Langevin equations (4.27), (4.28) are equivalent to the Smoluchowski
equation.





Next: Appendix A
Up: Stochastic processes
Previous: The Smoluchowski time scale
W.J. Briels
![]() of particles
which were at position
of particles
which were at position
![]() at time t=0. We assume that the
particles are at every instant of time in thermal equilibrium with respect
to their velocities. A flux will exist, given by
at time t=0. We assume that the
particles are at every instant of time in thermal equilibrium with respect
to their velocities. A flux will exist, given by
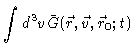
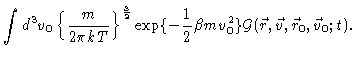
![]() .
To this end we multiply the Fokker-Planck
equation by
.
To this end we multiply the Fokker-Planck
equation by ![]() ,
average over the initial velocities, and integrate
over
,
average over the initial velocities, and integrate
over ![]() ,
obtaining
,
obtaining