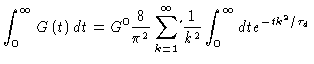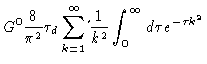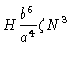Next: Index
Up: Dynamics of dense polymer
Previous: Monomer motion
Experimentally the shear relaxation modulus
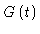 of a polymer melt turns
out to be like in Fig. 8.5.
of a polymer melt turns
out to be like in Fig. 8.5.
Figure 8.5:
Logarithmic plot of the time behavior of the shear relaxation modulus
|
|
We distinguish two regimes.
i)
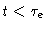
At short times the chain behaves like a 3-dimensional Rouse chain . Using Eq. 6.68 we find
which decays as t-1/2.8.1 At
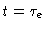 this possibility to relax ends. The only way for
the chain to relax any further is by breaking out of the tube.
this possibility to relax ends. The only way for
the chain to relax any further is by breaking out of the tube.
ii)
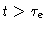
The stress that remains in the system is caused by the fact that the chains
are trapped in twisted tubes. By means of reptation the chain can break out of its tube. The newly generated
tube contains no stress. So, it is plausible to assume that the stress at
any time t is proportional to the fraction of the original tube that is
still part of the tube at time t. We'll call this fraction
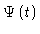 .
So,
.
So,
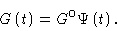 |
(8.23) |
On the reptation time scale, 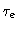 is practically zero, so we can set
is practically zero, so we can set
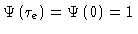 .
To make a smooth
transition from the Rouse regime to the reptation regime, we match Eq. (8.22) with Eq. (8.23) at
.
To make a smooth
transition from the Rouse regime to the reptation regime, we match Eq. (8.22) with Eq. (8.23) at
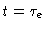 ,
yielding
,
yielding
| G0 |
= |
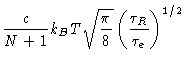 |
|
| |
= |
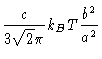 |
(8.24) |
We will now calculate
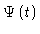 .
Take a look at
.
Take a look at
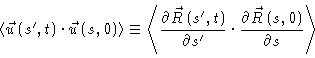 |
(8.25) |
The vector
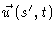 is the tangent to the
primitive chain, at segment
is the tangent to the
primitive chain, at segment
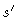 at time t. Because the primitive
chain has been parametrized with the contour length, we have from Eq.(8.1)
at time t. Because the primitive
chain has been parametrized with the contour length, we have from Eq.(8.1)
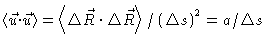 ; the non-existence of the
limit of
; the non-existence of the
limit of
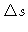 going to zero is a peculiarity of a Gaussian process.
Using Eq. 8.10 we calculate,
going to zero is a peculiarity of a Gaussian process.
Using Eq. 8.10 we calculate,
where we have used
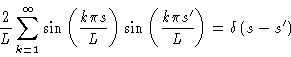 |
(8.28) |
Using this last equation, we also find
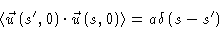 |
(8.29) |
This equation states that there is no correlation between the tangents to
the primitive chain at a segment s, and at another segment
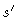 .
If we consider
.
If we consider
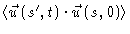 as a function of
as a function of
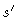 ,
at time t, we see that the original delta function has broadened and lowered.
However, the tangent
,
at time t, we see that the original delta function has broadened and lowered.
However, the tangent
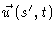 can only be
correlated to
can only be
correlated to
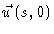 by means of diffusion of segment
by means of diffusion of segment
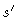 ,
during the time interval
,
during the time interval
![$\left[ 0,t\right] $](img995.gif) ,
to the place
where s was at time t=0, and still lies in the original tube. So,
,
to the place
where s was at time t=0, and still lies in the original tube. So,
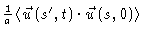 is the probability density that, at time t,
segment
is the probability density that, at time t,
segment
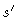 lies within the original tube at the place where swas initially. Integrating over
lies within the original tube at the place where swas initially. Integrating over
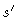 gives us the probability
gives us the probability
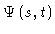 that at time t any segment lies within the
original tube at the place where segment s was initially. In other words,
the chance that the original tube segment s is still up-to-date, is
that at time t any segment lies within the
original tube at the place where segment s was initially. In other words,
the chance that the original tube segment s is still up-to-date, is
We have plotted this in Fig. 8.6.
Figure 8.6:
Development of
in time.
|
|
The fraction of the original tube that is still intact at time t, is
therefore given by
where the prime at the summation sign indicates that only terms with odd kshould occur in the sum. This formula shows why 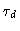 is the time
needed by the chain to reptate out if its tube; for
is the time
needed by the chain to reptate out if its tube; for
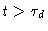 ,
,
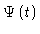 is falling to zero quickly.
is falling to zero quickly.
In conclusion we have found results that are in good agreement with Fig. 8.5. We see an initial drop proportional to t-1/2; after that a
plateau value G0 independent of N; and finally a
maximum relaxation time 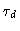 proportional to N3.
proportional to N3.
Finally, we are able to calculate the viscosity that is associated with the reptation model.
Using Eq. 6.53 we find
where H is a constant. We see that the viscosity is proportional to N3. This is close to the experimentally verified N3.4 behavior of polymer
melts with high molecular weight.
indextrans|seeconformation





Next: Index
Up: Dynamics of dense polymer
Previous: Monomer motion
W.J. Briels
![]() of a polymer melt turns
out to be like in Fig. 8.5.
of a polymer melt turns
out to be like in Fig. 8.5.
![]()
![]()
![]() .
So,
.
So,
![]() is practically zero, so we can set
is practically zero, so we can set
![]() .
To make a smooth
transition from the Rouse regime to the reptation regime, we match Eq. (8.22) with Eq. (8.23) at
.
To make a smooth
transition from the Rouse regime to the reptation regime, we match Eq. (8.22) with Eq. (8.23) at
![]() ,
yielding
,
yielding
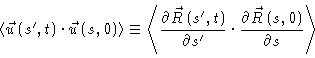
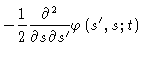
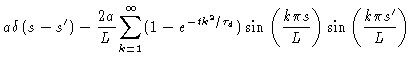
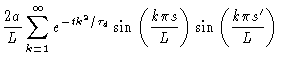
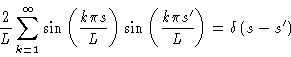
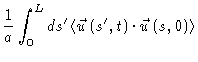
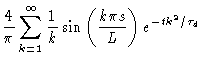
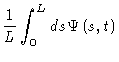
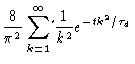
![]() proportional to N3.
proportional to N3.