We now must calculate
![]() under the
conditions given in Eqs. (6.50), (6.51) and (6.52). Let us write the flow like
under the
conditions given in Eqs. (6.50), (6.51) and (6.52). Let us write the flow like
![]() .
It is not difficult to understand that under these
conditions, the equations of motion read
.
It is not difficult to understand that under these
conditions, the equations of motion read
| = | 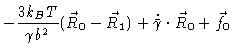 |
(6.58) | |
| = | 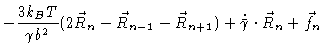 |
(6.59) | |
| = | 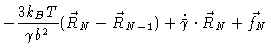 |
(6.60) | |
| = | (6.61) |
The reader who wishes to explicitly check the above equations, may start
with Eq. (4.2) and replace the particles velocity ![]() in
the friction force by its velocity relative to the average velocity, i.e. replace
in
the friction force by its velocity relative to the average velocity, i.e. replace
![]() by
by
![]() .
Going all the way to Eq. (4.39) he/she will find that also
there
.
Going all the way to Eq. (4.39) he/she will find that also
there
![]() is replaced by
is replaced by
![]() .
Next, putting
.
Next, putting
![]() equal to zero, and solving for
equal to zero, and solving for ![]() ,
he/she will find an extra term
,
he/she will find an extra term
![]() .
This finally will lead to an extra term in the Smoluchowski equation, which
can only be obtained from the Langevin equation Eq. (4.27) if it is augmented with a
term
.
This finally will lead to an extra term in the Smoluchowski equation, which
can only be obtained from the Langevin equation Eq. (4.27) if it is augmented with a
term
![]() on the right hand side.
on the right hand side.
We now continue our calculation of the stress tensor. To this end, we
transform to normal coordinates
![\begin{displaymath}S_{xy}(t)=\eta _{\mathrm{s}}
\dot{\gamma}+\frac{c}{N+1}k_{B}T...
...}\exp \left( -2\left( t-\tau \right) /\tau _{k}\right) \right]
\end{displaymath}](img820.gif) |
(6.67) |
In polymer melts, we must neglect the solvent contribution
![]() .
We recognize that the contribution of the Rouse chains to
the shear relaxation modulus is given by
.
We recognize that the contribution of the Rouse chains to
the shear relaxation modulus is given by
| = | 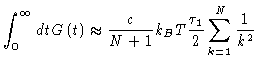 |
||
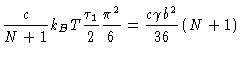 |
(6.69) |
In dilute solutions, we do not neglect the solvent contribution
![]() .
We combine Eqs. (6.53), (6.57) and (
6.66) to obtain an expression for the intrinsic viscosity ,
.
We combine Eqs. (6.53), (6.57) and (
6.66) to obtain an expression for the intrinsic viscosity ,
| = | 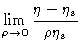 |
||
| = | 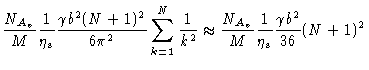 |
(6.70) |
We finish this section by calculating
![]() .
Integrating Eq. (6.62) we find
.
Integrating Eq. (6.62) we find
| (6.71) |
| = | 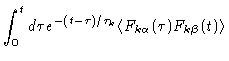 |
||
| = | 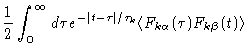 |
||
| = | 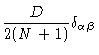 |
(6.72) |