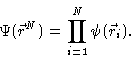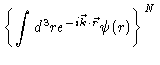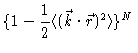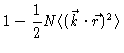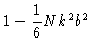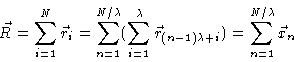Next: The Gaussian chain
Up: The Gaussian chain
Previous: Simple models
We shall discuss here the central limit theorem as applied to the calculation of the
distribution function of the end-to-end vector .
Consider a chain consisting of N independent bond vectors 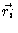 .
By this we mean that the probability density in configuration
space
.
By this we mean that the probability density in configuration
space
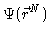 may be written as
may be written as
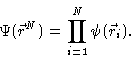 |
(3.1) |
Assume further that the bond vector probability density depends only on the
length of the bond vector, and has zero mean. For the second moment we write
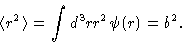 |
(3.2) |
The distribution of the end-to-end vector may be calculated according to
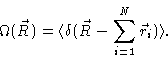 |
(3.3) |
The central limit theorem then states that
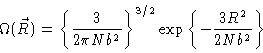 |
(3.4) |
i.e. that the end-to-end vector has Gaussian distribution.
In order to prove Eq. (3.4) we write
For k=0, the Fourier transform of 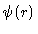 will be equal to one. Because
will be equal to one. Because
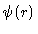 has zero mean and finite second moment, the Fourier transform of
has zero mean and finite second moment, the Fourier transform of 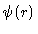 will have its maximum around k=0 and go to zero for large values
of k. Raising such a function to the N'th power leaves us with a
function that differs from zero only very close to the origin, and which may
be approximated by
will have its maximum around k=0 and go to zero for large values
of k. Raising such a function to the N'th power leaves us with a
function that differs from zero only very close to the origin, and which may
be approximated by
for small values of k, and by zero for the values of k where
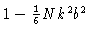 is negative. This again may be approximated by
is negative. This again may be approximated by
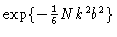 for all values of k. Then
for all values of k. Then
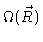 |
= |
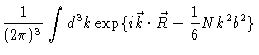 |
|
| |
= |
I(Rx) I(Ry) I(Rz) |
(3.7) |
| I(Rx) |
= |
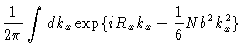 |
|
| |
= |
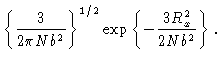 |
(3.8) |
Combining Eqs. (3.7) and (3.8) we get Eq. (
3.4).
Now apply the above result to a general RIS chain . To this end we write
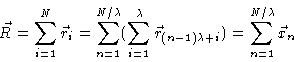 |
(3.9) |
i.e. we combine 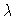 bond vectors into one new vector as in Fig. (
3.1) where
bond vectors into one new vector as in Fig. (
3.1) where
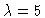 .
For
.
For 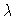 large enough the
distribution of these new vectors meets the conditions on
large enough the
distribution of these new vectors meets the conditions on
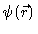 used to derive the central limit theorem. Notice that this holds true
because there are no long range excluded volume interactions in the RIS chain. Writing
used to derive the central limit theorem. Notice that this holds true
because there are no long range excluded volume interactions in the RIS chain. Writing
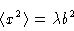 |
(3.10) |
we find that the distribution of the end-to-end vector is again given by
Eq. (3.4). We conclude that every model which does not
incorporate the long range excluded volume effect will have a Gaussianly
distributed end-to-end vector. It is an easy exercise to check that in this
case Eq. (1.45) holds true.
Figure 3.1:
Five bonds combined into one new vector.
|
|





Next: The Gaussian chain
Up: The Gaussian chain
Previous: Simple models
W.J. Briels
![]() .
By this we mean that the probability density in configuration
space
.
By this we mean that the probability density in configuration
space
![]() may be written as
may be written as