The Gaussian chain

The simplest model consistent with a Gaussian end-to-end vector distribution is one in which every bond vector itself is Gaussianly distributed . The probability distribution in configuration space then is

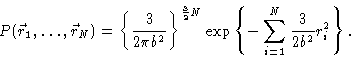$$P( \vec{r}_{1},\ldots ,\vec{r}_{N})=\left\{ \frac{3}{2\pi b^{... ...exp \left\{ -\sum_{i=1}^{N}\frac{3}{2b^{2}}r_{i}^{2}\right\} .$$ (3.11)

One may think of this model as a coarse grained  model of a polymer, where like in the previous section, every vector 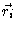$\vec{r}_{i}$ actually is the sum of 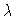$\lambda$ bond vectors, and where 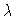$\lambda$ is large enough for 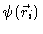$\psi (\vec{r}_{i})$ to be Gaussian. Usually the model is pictured as a chain of N beads connected by springs.

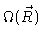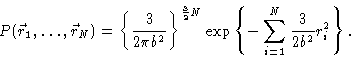
It is a useful exercise to calculate $\Omega (\vec{R})$ from Eqs. (3.3) and (3.11).