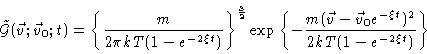Next: The Smoluchowski time scale
Up: Stochastic processes
Previous: The Langevin equation
An alternative way to study stochastic processes is by means of distribution
functions . Let
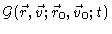 be the probability density to
find a particle at time t at position
be the probability density to
find a particle at time t at position 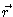 with velocity
with velocity 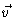 ,
given that at t=0 it was at position
,
given that at t=0 it was at position
 with velocity
with velocity
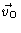 .
We shall demonstrate in Appendix A that this function satisfies
.
We shall demonstrate in Appendix A that this function satisfies
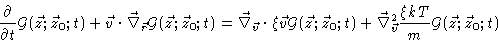 |
(4.14) |
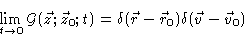 |
(4.15) |
where
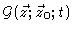 is short hand for
is short hand for
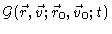 .
Eq. (4.14)
together with the initial value condition Eq. (4.15) is called
the Fokker-Planck equation .
.
Eq. (4.14)
together with the initial value condition Eq. (4.15) is called
the Fokker-Planck equation .
We shall not treat this equation any further here, except for one quick
remark. The probability to find the particle at time t with velocity 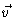 ,
at any position, given it was at t=0 at position
,
at any position, given it was at t=0 at position
 with velocity
with velocity
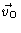 is given by
is given by
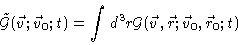 |
(4.16) |
where we have assumed the system is translational invariant, i.e. both
sides of Eq. (4.16) are independent of
 .
Integrating Eq. (4.14) with respect to
.
Integrating Eq. (4.14) with respect to 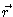 we get
we get
We may easily obtain the solution to this equation by using the results of
the previous section. To this end we notice that
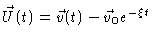 according to Eq. (4.4) is a sum of many
random vectors. According to the central limit theorem therefore it must have a Gaussian
distribution. The first and second moments are given by
according to Eq. (4.4) is a sum of many
random vectors. According to the central limit theorem therefore it must have a Gaussian
distribution. The first and second moments are given by
where we have used the fluctuation-dissipation theorem in the form
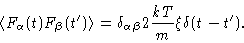 |
(4.21) |
Using Eqs. (4.19) and (4.20) we may write
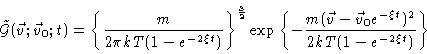 |
(4.22) |
Although it is a tedious task, it is not difficult to check that this result
indeed is the solution to Eqs. (4.17) and (4.18).





Next: The Smoluchowski time scale
Up: Stochastic processes
Previous: The Langevin equation
W.J. Briels
![]() be the probability density to
find a particle at time t at position
be the probability density to
find a particle at time t at position ![]() with velocity
with velocity ![]() ,
given that at t=0 it was at position
,
given that at t=0 it was at position
![]() with velocity
with velocity
![]() .
We shall demonstrate in Appendix A that this function satisfies
.
We shall demonstrate in Appendix A that this function satisfies
![]() ,
at any position, given it was at t=0 at position
,
at any position, given it was at t=0 at position
![]() with velocity
with velocity
![]() is given by
is given by