Next: The Smoluchowski equation
Up: Stochastic processes
Previous: The Fokker-Planck equation
From Eq. (4.8) we see that the particle loses its memory of its
initial velocity after a time span
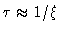 .
Using equipartition its initial velocity may be put equal to
.
Using equipartition its initial velocity may be put equal to
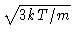 .
The distance it travels, divided by its diameter then is
.
The distance it travels, divided by its diameter then is
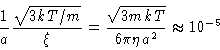 |
(4.23) |
where the value 10-5 refers to normal colloidal particles. We see that
the particles have hardly moved at the time possible velocity gradients have
relaxed to equilibrium. When we are interested in timescales on which
particle configurations change, like in dynamic light scattering experiments , we may restrict our attention to the space
coordinates, and average over the velocities.
A very crude way to arrive at the equations of motion is the following. On
the timescale referred to above, and which is called the Smoluchowski time
scale , the average velocity is zero, or constant
in case we apply an external force. Eq. (4.2) then becomes
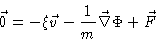 |
(4.24) |
where
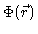 is the external potential . Rewriting this, and using the
fluctuation-dissipation theorem we get
is the external potential . Rewriting this, and using the
fluctuation-dissipation theorem we get
These equations are correct when D is independent of the position of the
particle. However it is clear that the random term now refers to a
completely different timescale than in the original Langevin equation ; nevertheless
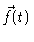 is obtained here from
is obtained here from
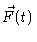 by dividing the latter by
by dividing the latter by 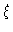 ,
meaning that the ''derivation'' given here must be wrong. The flaw
occurs when the instantaneous acceleration is put equal to zero in Eq. (4.24). In fact it is the average acceleration which should be put
equal to zero.
,
meaning that the ''derivation'' given here must be wrong. The flaw
occurs when the instantaneous acceleration is put equal to zero in Eq. (4.24). In fact it is the average acceleration which should be put
equal to zero.
In the next section we shall derive the Smoluchowski equation, governing the
time development of the distribution of particles on the Smoluchowski
timescale. In Appendix C we shall then show that the correct Langevin
equations which lead to the Smoluchowski equation are:
In our treatment of the Rouse chain in Chapter 6 the diffusion constant will
be independent of 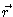 ,
in which case Eqs. (4.27) and (4.28) are equivalent to Eqs. (4.25) and (4.26).
,
in which case Eqs. (4.27) and (4.28) are equivalent to Eqs. (4.25) and (4.26).





Next: The Smoluchowski equation
Up: Stochastic processes
Previous: The Fokker-Planck equation
W.J. Briels
![]() .
Using equipartition its initial velocity may be put equal to
.
Using equipartition its initial velocity may be put equal to
![]() .
The distance it travels, divided by its diameter then is
.
The distance it travels, divided by its diameter then is