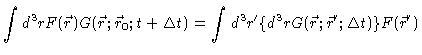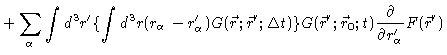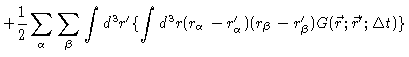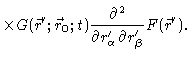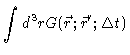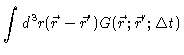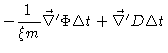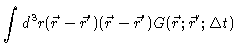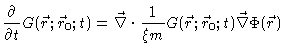



Next: Hydrodynamics
Up: Stochastic processes
Previous: Appendix B
In this appendix we shall derive the Smoluchowski equation , starting from the Langevin equation (4.27), (4.28).
Using exactly the same method as in appendix A, but now applied to
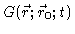 we arrive at
we arrive at
Using
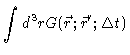 |
= |
1 |
(4.76) |
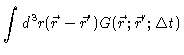 |
= |
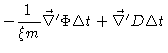 |
(4.77) |
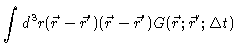 |
= |
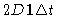 |
(4.78) |
which follow from Eqs. (4.27) and (4.28), and
following the same strategy as in appendix A we arrive at
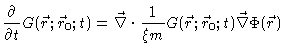 |
| |
|
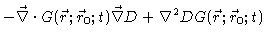 |
(4.79) |
It is not difficult to show that the last two terms together yield
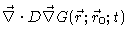 ,
which proves the
equivalence of Eqs. (4.27), (4.28) and Eqs. (4.32), (4.33).
,
which proves the
equivalence of Eqs. (4.27), (4.28) and Eqs. (4.32), (4.33).




Next: Hydrodynamics
Up: Stochastic processes
Previous: Appendix B
W.J. Briels
![]() we arrive at
we arrive at