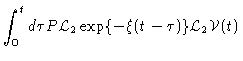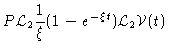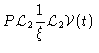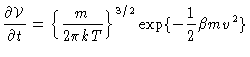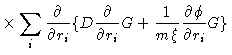Next: Appendix C
Up: Stochastic processes
Previous: Appendix A
In this appendix we derive the Smoluchowski equation directly from the Fokker-Planck equation . This appendix will be rather technical.
In a potential field the Fokker-Planck equation reads
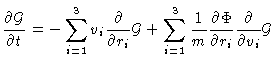 |
| |
|
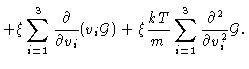 |
(4.52) |
On the Smoluchowski timescale we are interested in
We first notice that 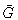 also satisfies Eq. (4.52), but
with initial value condition
also satisfies Eq. (4.52), but
with initial value condition
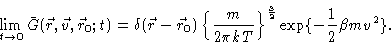 |
(4.55) |
For large values of 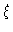 we expect that the velocities will continually be
in thermal equilibrium, i.e. that the equilibration time of the velocities
is small on the Brownian timescale. We therefore expect that
we expect that the velocities will continually be
in thermal equilibrium, i.e. that the equilibration time of the velocities
is small on the Brownian timescale. We therefore expect that
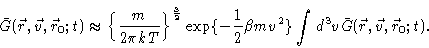 |
(4.56) |
From Eq. (4.55) we see that this certainly holds true in the
limit of t going to zero.
We now define the projection operator P by
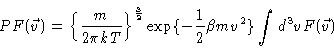 |
(4.57) |
where
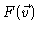 may be any function of
may be any function of 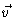 .
We write the
Fokker-Planck equation as
.
We write the
Fokker-Planck equation as
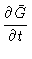 |
= |
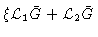 |
(4.58) |
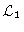 |
= |
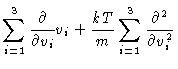 |
(4.59) |
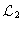 |
= |
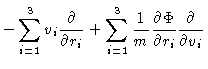 |
(4.60) |
The projection can easily be shown to have the following properties
| P2 |
= |
P |
(4.61) |
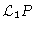 |
= |
0 |
(4.62) |
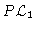 |
= |
0 |
(4.63) |
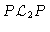 |
= |
0 |
(4.64) |
We shall now derive the equation of motion of 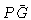 .
The Smoluchowski
equation, i.e. the equation of motion of
.
The Smoluchowski
equation, i.e. the equation of motion of
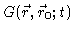 then
follows at once from
then
follows at once from
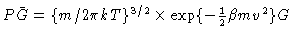
Defining
we get from Eq. (4.58)
We now solve Eq. (4.68) using
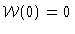 ,
and introduce
the result in Eq. (4.67):
,
and introduce
the result in Eq. (4.67):
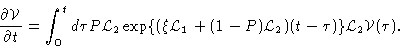 |
(4.69) |
This result is exact, and therefore not very useful.
We shall now simplify Eq. (4.69) by means of some
approximations based on physical grounds. First, since we want to describe
the Smoluchowski timescale, we let 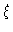 be large, obtaining
be large, obtaining
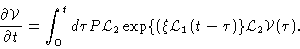 |
(4.70) |
Next we invoke the Markov property; the coordinates develop slowly, meaning
that the system quickly loses its memory of the past, and
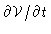 can only depend on the value of
can only depend on the value of
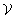 at time tand not on its values at earlier times
at time tand not on its values at earlier times
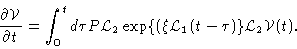 |
(4.71) |
It is a simple but rather tedious task to prove that
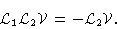 |
(4.72) |
Using this in Eq. (4.71) yields
where in the last step we have used the overdamped condition
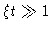 .
Introducing the definition of P and
.
Introducing the definition of P and
 ,
and working through
all derivations and integrals one obtains
,
and working through
all derivations and integrals one obtains
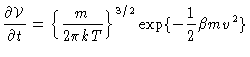 |
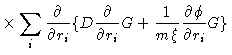 |
|
|
(4.74) |
which is recognized as the Smoluchowski equation after using
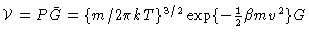 .
.





Next: Appendix C
Up: Stochastic processes
Previous: Appendix A
W.J. Briels
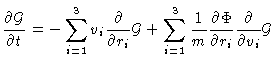
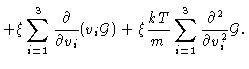
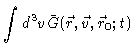
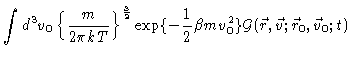
![]() be large, obtaining
be large, obtaining