Hydrodynamics describes the flow properties of viscoelastic materials. The basic quantities are the density
![]() and velocity
and velocity
![]() .
Here
.
Here
![]() is
the density of the material which at time t happens to be at position
is
the density of the material which at time t happens to be at position ![]() .
Similarly
.
Similarly
![]() is the velocity of the material
which at time t is at position
is the velocity of the material
which at time t is at position ![]() .
A consequence of describing the
flow field this way, is that for example
.
A consequence of describing the
flow field this way, is that for example
![]() and
and
![]() are the densities of two
different amounts of material. If we want to know the change with time of
the density of a given amount of material we shall write
are the densities of two
different amounts of material. If we want to know the change with time of
the density of a given amount of material we shall write
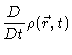 |
= | 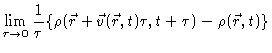 |
|
| = | 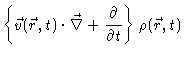 |
(5.1) |
A second important concept in hydrodynamics is that of friction . Suppose we have a linear flow field like in Fig. (5.1), where the arrows indicate the velocities. The only nonzero
velocity component is in the y-direction, and it only depends on z. Now
look at a volume element at (x,y,z). It has a velocity vy(z) which is
larger than the velocity
vy(z-dz) of the volume element just below it.
As a result the element at (x,y,z) will be slowed down and the one at
(x,y,z-dz) will be accelerated. Both forces will be proportional to
![]() and to the surface dxdy, with constant of
proportionality
and to the surface dxdy, with constant of
proportionality ![]() .
Similarly the volume element at (x,y,z) will be
accelerated by the one at
(x,y,z+dz). In total our volume element will
feel a force in the y-direction given by
.
Similarly the volume element at (x,y,z) will be
accelerated by the one at
(x,y,z+dz). In total our volume element will
feel a force in the y-direction given by
| Fy | = | 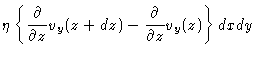 |
|
| = | 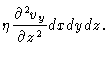 |
(5.2) |
| FyP | = | P(y)dxdz-P(y+dy)dxdz | |
| = | 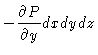 |
(5.3) |