




Next: A moving sphere in
Up: Hydrodynamics
Previous: Introduction
In this section we shall present two important equations governing the
dynamics of fluid flow. First we obtain the equation describing the
conservation of mass. Next we present the equation of motion. In order to do
this we have to generalize the concept of viscosity as introduced in the
previous section.
Consider a volume element with edges (dx,0,0), (0,dy,0) and (0,0,dz).
If we follow the mass in our volume element along the flow during a short
time 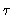 ,
the line element (dx,0,0) will transform into
,
the line element (dx,0,0) will transform into
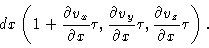 |
(5.4) |
Analogous equations hold for the other line elements. The volume after time 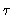 will be
will be
As a result we have
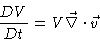 |
(5.6) |
or using
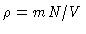
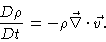 |
(5.7) |
This equation describes the conservation of mass .
We shall now generalize the concept of viscosity as it was given in section
1. Consider a surface element of size dA, and normal 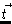 .
Let
.
Let 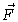 be the force exerted by the fluid below the surface
element on the fluid above the surface element. Then we define the stress
tensor S by
be the force exerted by the fluid below the surface
element on the fluid above the surface element. Then we define the stress
tensor S by
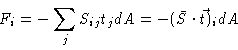 |
(5.8) |
The total force in i-direction on a given volume element at (x,y,z) then
is
where x1=x, x2=y and x3=z. In vector notation
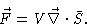 |
(5.10) |
Since S will turn out to be symmetric, there is no ambiguity in this
notation. This force accelerates the mass in our volume element, which is 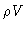 .
Newton's second law then reads
.
Newton's second law then reads
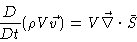 |
(5.11) |
Writing
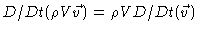 ,
because
,
because 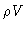 is
constant along the flow, and dividing by V we get
is
constant along the flow, and dividing by V we get
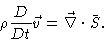 |
(5.12) |
This is the Navier-Stokes equation .
Many fluids may be described by assuming that the stress tensor S consists
of a part, which is independent of the velocity, and a part which depends
linearly on the derivatives
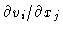 .
In
hydrodynamics it is shown that the most general stress tensor having these properties then reads
.
In
hydrodynamics it is shown that the most general stress tensor having these properties then reads
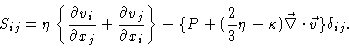 |
(5.13) |
Here 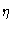 is the shear viscosity ,
is the shear viscosity , 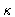 is the bulk viscosity , and P the pressure .
is the bulk viscosity , and P the pressure .
Many flow fields of interest may be described assuming that the fluid is
incompressible , i.e. that the density along the flow is
constant. In that case
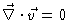 ,
as follows from Eq. (5.7).
Assuming moreover that the velocities are small, and that the second order
non-linear term
,
as follows from Eq. (5.7).
Assuming moreover that the velocities are small, and that the second order
non-linear term
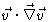 may be neglected we
obtain Stokes equations for incompressible flow
may be neglected we
obtain Stokes equations for incompressible flow
These are the equations that we are going to use in the next two sections.





Next: A moving sphere in
Up: Hydrodynamics
Previous: Introduction
W.J. Briels
![]() ,
the line element (dx,0,0) will transform into
,
the line element (dx,0,0) will transform into
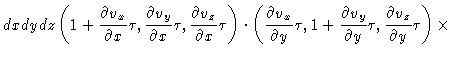
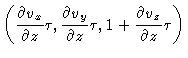
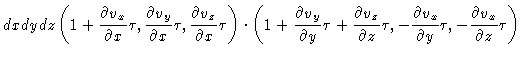
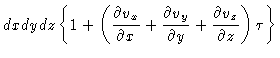
![]() .
Let
.
Let ![]() be the force exerted by the fluid below the surface
element on the fluid above the surface element. Then we define the stress
tensor S by
be the force exerted by the fluid below the surface
element on the fluid above the surface element. Then we define the stress
tensor S by
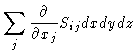
![]() .
In
hydrodynamics it is shown that the most general stress tensor having these properties then reads
.
In
hydrodynamics it is shown that the most general stress tensor having these properties then reads
![]() ,
as follows from Eq. (5.7).
Assuming moreover that the velocities are small, and that the second order
non-linear term
,
as follows from Eq. (5.7).
Assuming moreover that the velocities are small, and that the second order
non-linear term
![]() may be neglected we
obtain Stokes equations for incompressible flow
may be neglected we
obtain Stokes equations for incompressible flow