![\scalebox{0.5}{\includegraphics[18,538][577,819]{fig1_1.eps}}](img1.gif)
|
Polymers are huge molecules constructed out of many identical building blocks called monomers. Here we shall restrict ourselves to linear molecules in which every monomer has one successor and/or predecessor. The number of monomers per polymer may vary from a few hundreds to many thousands.
The simplest example of a polymer is drawn below.
The polymer is drawn here in the trans conformation . Many other conformations exist, and it is the aim of the RIS model to describe the statistics of these conformations.
We shall describe the conformation of the polymer by giving the position
vectors of its backbone atoms, in this case the carbon
atoms. The positions of the remaining atoms then usually follow by simple
chemical rules. So, suppose we have N+1 monomers, then we have N+1position vectors
Alternatively we may also use the N-2 dihedral angles
Now first consider the case of n-butane . We have but one dihedral, and the energy as a function of this angle is drawn below.
The conformation with
![]() is called the trans
conformation , the one with
is called the trans
conformation , the one with
![]() is
called gauche plus (g+) , and the one with
is
called gauche plus (g+) , and the one with
![]() is called gauche minus (g-) . Notice that at room temperature only the
three minima will be populated which makes it possible to restrict interest
to three conformations called t,g+ and g-.
is called gauche minus (g-) . Notice that at room temperature only the
three minima will be populated which makes it possible to restrict interest
to three conformations called t,g+ and g-.
Now let us try to write down the energy of a polymer as a function of the
angles
![]() .
In order to do so we start with the molecule in its
all trans conformation i.e.
.
In order to do so we start with the molecule in its
all trans conformation i.e.
![]() for all i. Next we
successively bring the angles
for all i. Next we
successively bring the angles
![]() to their actual values. Every angle will then contribute to the
total energy like in the case of butane i.e.
to their actual values. Every angle will then contribute to the
total energy like in the case of butane i.e.
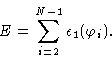 |
(1.1) |
It will be clear that the above is also only part of the story because we have neglected the possibility that monomers i and i+n (n>4) will occupy the same position. We may say that we have included the short range excluded volume effect , but not the long range excluded volume. Short range and long range here refer to the distance along the chain. Inclusion of long range effects makes the problem virtually intractable, so we stop at the level of Eq. (1.2). We shall say a few qualitative things about the excluded volume effect later on.