| (5.42) |
Now consider a suspension of colloidal particles. The motion of a given particle induces a flow field in the solvent, which will be felt by all the other particles. As a result these particles experience a force which is said to result from hydrodynamic interaction with the original particle.
The hydrodynamic problem now is to find a flow field satisfying Eqs. (5.16) and (5.17) together with the boundary conditions
| (5.42) |
| (5.43) |
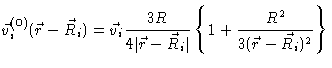 | |||
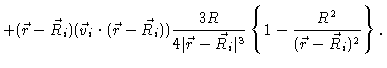 |
(5.44) | ||
We shall first discuss the situation for only two particles in the solvent.
In the neighbourhood of particle one the velocity field may be written as
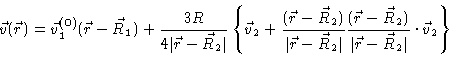 |
(5.45) |
We now notice that the correction that we have applied to the flow field in order to satisfy the boundary conditions at the surface of particle one is of order R/ R21. Its strength in the neighbourhood of particle two is then of order (R/R21)2, and need therefore not be taken into account when the flow field is adapted to the boundary conditions at particle two.
The flow field around particle one is now given by Eqs. (5.47)
and (5.48). The last term in Eq. (5.47) does not
contribute to the stress tensor. The force exerted by the fluid on particle
one then equals
![]() .
A similar
result holds for particle two. In full we have
.
A similar
result holds for particle two. In full we have
| = | 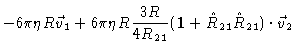 |
(5.49) | |
| = | 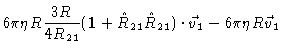 |
(5.50) |
| = |  |
(5.51) | |
| = | 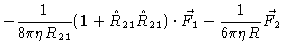 |
(5.52) |
When more than two particles are present in the fluid, corrections resulting
from n-body interactions ![]() are of order
(R/Rij)2 or
higher and need not be taken into account. The above treatment therefore
generalizes to
are of order
(R/Rij)2 or
higher and need not be taken into account. The above treatment therefore
generalizes to