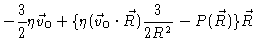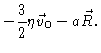Next: Hydrodynamic interaction in colloidal
Up: Hydrodynamics
Previous: Navier-Stokes equations
Consider a sphere of radius R, moving with velocity
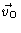 in a
quiescent fluid . Referring all coordinates and velocities to a frame
which moves with velocity
in a
quiescent fluid . Referring all coordinates and velocities to a frame
which moves with velocity
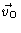 relative to the fluid transforms the problem into one of a
resting sphere in a fluid which, at large distances from the sphere, moves
with constant velocity
relative to the fluid transforms the problem into one of a
resting sphere in a fluid which, at large distances from the sphere, moves
with constant velocity
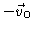 .
.
Our velocity field will be stationary. The Stokes equations then read
with boundary conditions
As a first step towards the solution, we take the divergence of Eq. (5.16). Making use of the incompressibility equation (5.17) we then get
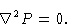 |
(5.20) |
Now, notice that the flow field will be linear in
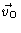 .
From Eq. (5.16) it follows that
.
From Eq. (5.16) it follows that
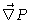 will then also be linear in
will then also be linear in
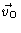 .
Moreover
.
Moreover
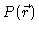 must be
invariant under a rotation of both the coordinate frame and
must be
invariant under a rotation of both the coordinate frame and
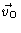 .
Therefore we write
.
Therefore we write
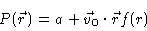 |
(5.21) |
Introducing this into Eq. (5.20) we get
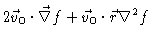 |
= |
0 |
|
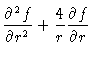 |
= |
0 |
(5.22) |
Solving this under the condition
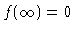 ,
we get
f(r)=br-3, and
,
we get
f(r)=br-3, and
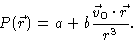 |
(5.23) |
Eq. (5.16) now reads
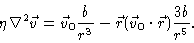 |
(5.24) |
Now again, we notice that
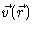 must be linear in
must be linear in
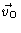 .
Moreover it must transform like
.
Moreover it must transform like
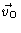 and
and 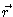 under a
joint rotation of
under a
joint rotation of
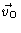 and the coordinate frame. Therefore
and the coordinate frame. Therefore
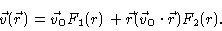 |
(5.25) |
Introducing this expression into Eq. (5.24), we get
from which
The boundary conditions for these equations are
| F1(R) |
= |
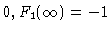 |
(5.29) |
| F2(R) |
= |
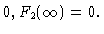 |
(5.30) |
We first solve Eq. (5.28) under the condition Eq. (5.30). Solutions to the homogeneous equation are cr-5; a
particular solution is
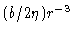 .
According to the boundary
condition Eq. (5.30) we then get
.
According to the boundary
condition Eq. (5.30) we then get
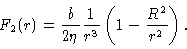 |
(5.31) |
Equation (5.27) now reads
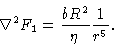 |
(5.32) |
Solutions to the homogeneous equation are
-1+cr-1; a particular
solution is
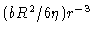 .
The boundary conditions Eq. (5.29) then lead to
.
The boundary conditions Eq. (5.29) then lead to
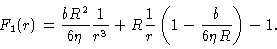 |
(5.33) |
Finally we have to fulfill the incompressibility equation
Introducing F1 and F2 we find
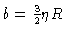 .
.
We now introduce F1 and F2 from Eqs. (5.33) and (5.31), together with
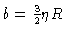 into Eq. (5.25), and add
into Eq. (5.25), and add
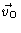 to get the flow field around a sphere
at the origin, moving with velocity
to get the flow field around a sphere
at the origin, moving with velocity
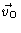 in a quiescent fluid.
in a quiescent fluid.
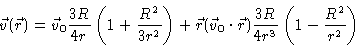 |
(5.35) |
One easily checks the boundary conditions
We shall now use this flow field to calculate the force exerted by the fluid on the
particle.
According to Eq. (5.8) the force exerted by the fluid on the
sphere is given by
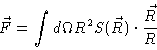 |
(5.38) |
where
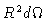 is a surface element on the sphere. The stress tensor
is given by Eq. (5.13), which in the case of an incompressible
fluid reads
is a surface element on the sphere. The stress tensor
is given by Eq. (5.13), which in the case of an incompressible
fluid reads
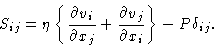 |
(5.39) |
Using the flow field given in Eq. (5.35) and the pressure given
in Eq. (5.23), where
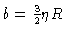 ,
we calculate
,
we calculate
Introducing this into Eq. (5.38) and performing the integral we
obtain
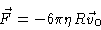 |
(5.41) |
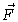 is known as the Stokes friction .
is known as the Stokes friction .





Next: Hydrodynamic interaction in colloidal
Up: Hydrodynamics
Previous: Navier-Stokes equations
W.J. Briels
![]() in a
quiescent fluid . Referring all coordinates and velocities to a frame
which moves with velocity
in a
quiescent fluid . Referring all coordinates and velocities to a frame
which moves with velocity
![]() relative to the fluid transforms the problem into one of a
resting sphere in a fluid which, at large distances from the sphere, moves
with constant velocity
relative to the fluid transforms the problem into one of a
resting sphere in a fluid which, at large distances from the sphere, moves
with constant velocity
![]() .
.
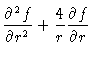
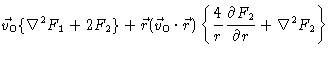
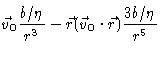
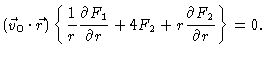
![]() into Eq. (5.25), and add
into Eq. (5.25), and add
![]() to get the flow field around a sphere
at the origin, moving with velocity
to get the flow field around a sphere
at the origin, moving with velocity
![]() in a quiescent fluid.
in a quiescent fluid.