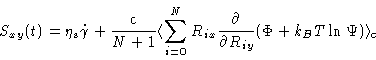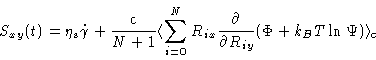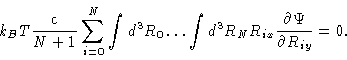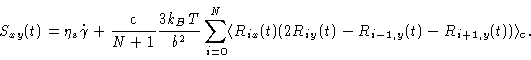



Next: C. Calculation of the
Up: Viscosity of a dilute
Previous: A. Shear flow
The beads in our polymer are assumed to be point particles. The second term
in Eq. (5.64) is proportional to the volume fraction of beads,
and therefore equals zero. The element Sxy(t) of the stress tensor then reads
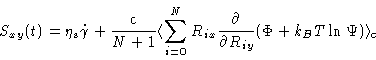 |
(6.54) |
where
c is the monomer concentration. The 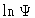 term yields
term yields
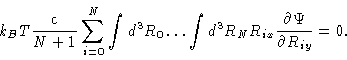 |
(6.55) |
So, we are left with
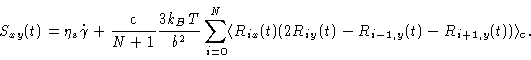 |
(6.56) |
We next introduce the normal mode expansion Eq. (6.24), and go
through the usual analysis; finding
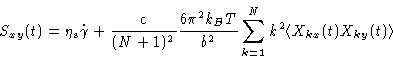 |
(6.57) |
From now on we omit the subscript
c at the averaging brackets,
because it serves no purpose anymore.
W.J. Briels