




Next: Correlation of the end-to-end
Up: The Rouse chain
Previous: The Rouse chain
We shall now solve the equations (6.3) to (6.6) . We first solve them leaving out the fluctuating
forces. The equations of motion then form a linear set of (3N+3) first
order differential equations, whose general solutions are sums of (3N+3)independent specific solutions.
As a specific solution we try
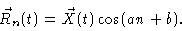 |
(6.10) |
The equations of motion then read
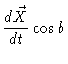 |
= |
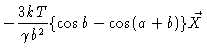 |
(6.11) |
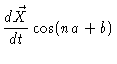 |
= |
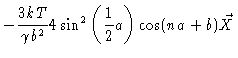 |
(6.12) |
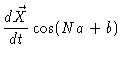 |
= |
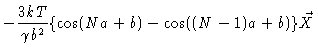 |
(6.13) |
where we have used
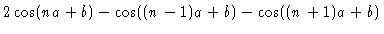 |
| |
= |
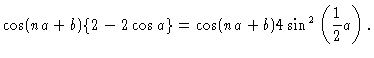 |
(6.14) |
In order for equations (6.11) to (6.13) to be
consistent we need
This may be rewritten as
We find independent solutions from
| a-b |
= |
b |
(6.19) |
| (N+1)a+b |
= |
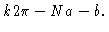 |
(6.20) |
So, finally
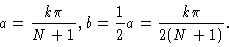 |
(6.21) |
The specific solution Eq. (6.10), with a and b from Eq. (
6.21) decouple the set of differential equations.
In the following we shall frequently make use of
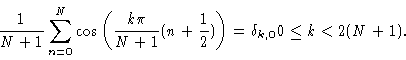 |
(6.22) |
This is evident when k=0 or k=N+1. In the remaining cases the sum may be
evaluated by using
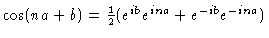 .
The result then is
.
The result then is
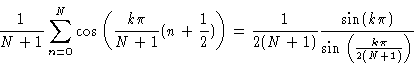 |
(6.23) |
which is consistent with Eq. (6.22).
We now turn to the solution of Eqs. (6.3) to (6.6
). To this end we write
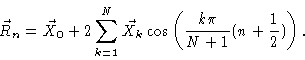 |
(6.24) |
The factor of two in front of the summation is only for reasons of
convenience. Using Eq. (6.22) we may invert this to
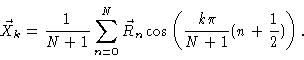 |
(6.25) |
The equations of motion then read
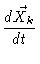 |
= |
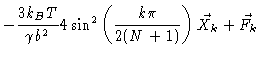 |
(6.26) |
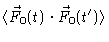 |
= |
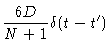 |
(6.27) |
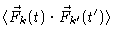 |
= |
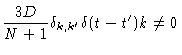 |
(6.28) |
Eqs. (6.27) and (6.28) were obtained from Eq. (6.6) and Eq. (6.22) by using
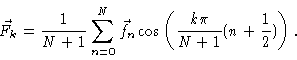 |
(6.29) |
We have finally arrived at a decoupled set of 3(N+1) stochastic
differential equations. In fact all of them are similar to our first
stochastic differential equation (4.2). They only differ in
their friction coefficients , and in the characteristics of the random
forces.
Using Eq. (6.22) we easily see that
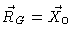 .
Eqs. (6.26) and (6.27)
for k=0 read
.
Eqs. (6.26) and (6.27)
for k=0 read
from which we get again the diffusion coefficient of the centre of mass as given
in Eq. (6.9).
The specific solutions that we have found are called the normal modes of the chain.
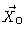 describes the motion of the centre of gravity. The other modes
describe vibrations of the chain leaving the centre of mass unchanged.
describes the motion of the centre of gravity. The other modes
describe vibrations of the chain leaving the centre of mass unchanged.
In the applications ahead of us, our results will always be expressed as
sums over normal modes, which sums will always be dominated by the
contributions from the modes with small k, i.e. those with large
wavelength. We therefore approximate Eq. (6.26) by
These equations apply when 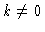 .
The characteristic time
.
The characteristic time 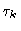 is
given by
is
given by
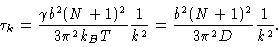 |
(6.34) |





Next: Correlation of the end-to-end
Up: The Rouse chain
Previous: The Rouse chain
W.J. Briels
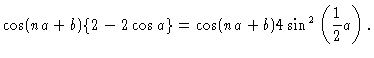
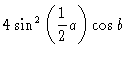
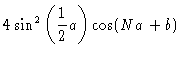
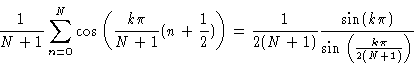
![]() .
Eqs. (6.26) and (6.27)
for k=0 read
.
Eqs. (6.26) and (6.27)
for k=0 read
![]() describes the motion of the centre of gravity. The other modes
describe vibrations of the chain leaving the centre of mass unchanged.
describes the motion of the centre of gravity. The other modes
describe vibrations of the chain leaving the centre of mass unchanged.