Next: B. The stress tensor
Up: Viscosity of a dilute
Previous: Viscosity of a dilute
In this final section we calculate the viscosity of a dilute
polymer solution. Shear flows, for which the velocity components are given
by
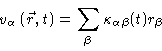 |
(6.48) |
are commonly used for studying viscoelastic properties. If the shear rates
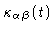 are small
enough, the stress tensor depends linearly on
are small
enough, the stress tensor depends linearly on
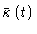 and can be written as
and can be written as
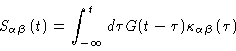 |
(6.49) |
where G(t) is called the shear relaxation modulus .
An important special case is a stepwise shear flow, which is switched on at t=0:
| vx(t) |
= |
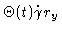 |
(6.50) |
| vy(t) |
= |
0 |
(6.51) |
| vz(t) |
= |
0 |
(6.52) |
where
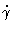 is called the shear rate and
is called the shear rate and 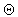 is the Heaviside
function (
is the Heaviside
function (
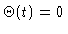 for t<0,
for t<0,
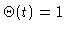 for
for 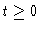 ). From Eqs. (
5.13) and (6.49) we see that
). From Eqs. (
5.13) and (6.49) we see that
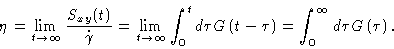 |
(6.53) |
The limit
 must be taken because during the early
stages elastic stresses are built up.
must be taken because during the early
stages elastic stresses are built up.
The calculation now consists of two steps. First we shall bring Eq. (5.64) into a form applicable to the present case. In the second
step we shall formulate the Langevin approach of section 6.3 in the case
when the system is under shear, and calculate the stress tensor.





Next: B. The stress tensor
Up: Viscosity of a dilute
Previous: Viscosity of a dilute
W.J. Briels