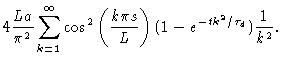Next: Viscoelastic behavior
Up: Dynamics of dense polymer
Previous: Mathematical definition of the
We shall now demonstrate that according to our model the mean quadratic
displacement of a typical monomer behaves like
in Fig. (8.3). This behaviour has been qualitatively verified by
computer simulations for times up to somewhere in the third regime. Of
course the final regime should be simple diffusive motion. The important
prediction is the dependence of the diffusion constant on N.
Figure 8.3:
Double-logarithmic plot of the mean square displacement,
, in case of the
reptation model (solid line) and the Rouse model (dashed).
|
|
In Fig. (8.3)  is the Rouse time which is equal to
is the Rouse time which is equal to  in chapter 6. The meaning
of
in chapter 6. The meaning
of  and
and 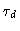 will become clear in the remaining part of
this section.
will become clear in the remaining part of
this section.
We shall now treat the different regimes in Fig. (8.3) one after
another.
i)
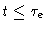 .
.
At short times a Rouse bead doesn't know about any tube constraints.
According to section 6.5 then
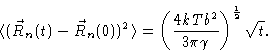 |
(8.3) |
Consistent with the Gaussian character of the primitive chain we may suppose
that the diameter of the tube is equal to a. Once the segment has moved a distance
a, it will feel the constraints of the tube, and a new regime will set in.
The time at which this happens is given by
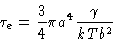 |
(8.4) |
Notice that this is independent of N.
ii)
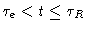 .
.
On the time and distance scale we are looking now, the bead performs random
motions, still constrained by the fact that the monomer is a part of a chain
because
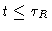 .
Orthogonally to the primitive chain these motions
do not lead to any displacement, because of the constraints implied by the
tube. Only along the primitive chain the bead may diffuse free of any other
constraint than the one implied by the fact that it belongs to a chain. The
diffusion therefore is given by the 1-dim. analog of Eq. (6.47) or Eq. (8.3).
.
Orthogonally to the primitive chain these motions
do not lead to any displacement, because of the constraints implied by the
tube. Only along the primitive chain the bead may diffuse free of any other
constraint than the one implied by the fact that it belongs to a chain. The
diffusion therefore is given by the 1-dim. analog of Eq. (6.47) or Eq. (8.3).
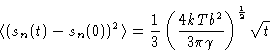 |
(8.5) |
where sn(t) is the position of bead n along the primitive chain at
time t. It is assumed here that for times
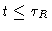 the chain as a
whole does not move, i.e. that the primitive chain does not change. Using
Eq. (8.1) then
the chain as a
whole does not move, i.e. that the primitive chain does not change. Using
Eq. (8.1) then
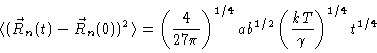 |
(8.6) |
where we have assumed
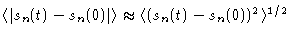 .
.
iii)
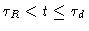 .
.
The bead still moves along the tube diameter. Now however
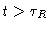 ,
which means that we should use the 1-dim. analog of Eq. (6.45
).
,
which means that we should use the 1-dim. analog of Eq. (6.45
).
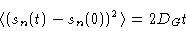 |
(8.7) |
Again assuming that the tube doesn't change appreciably during time t, we
get
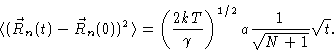 |
(8.8) |
From our treatment it is clear that  is the time it takes for the
chain to create a tube which is uncorrelated to the old one. We will
calculate
is the time it takes for the
chain to create a tube which is uncorrelated to the old one. We will
calculate  in the next paragraph.
in the next paragraph.
iv)
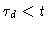 .
.
This is the regime in which reptation dominates. On this time and space scale we may attribute
to every bead a definite value of s. We then want to calculate
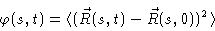 |
(8.9) |
where
 is the position of bead s at time t.
is the position of bead s at time t.
Figure 8.4:
Motion of the primitive chain along its contour.
|
|
In order to calculate
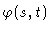 it is useful to introduce
it is useful to introduce
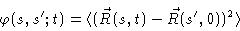 |
(8.10) |
i.e. the mean square distance between bead s at time t and bead
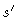 at time zero. According to Fig. (8.4), for all s,
except s=a and s=L, we have
at time zero. According to Fig. (8.4), for all s,
except s=a and s=L, we have
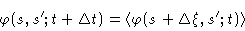 |
(8.11) |
where
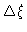 according to the definition of the primitive chain in
section 2 is a stochastic variable. The average on the right hand side has
to be taken over the distribution of
according to the definition of the primitive chain in
section 2 is a stochastic variable. The average on the right hand side has
to be taken over the distribution of
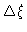 .
Expanding the right hand
side of Eq. (8.11) we get
.
Expanding the right hand
side of Eq. (8.11) we get
Introducing this into Eq. (8.11) and taking the limit for 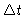 going to zero, we get
going to zero, we get
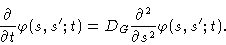 |
(8.13) |
In order to complete our description of reptation we have to find the
boundary conditions going with this diffusion equation. We will demonstrate
that these are given by
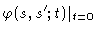 |
= |
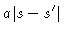 |
(8.14) |
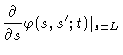 |
= |
a |
(8.15) |
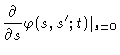 |
= |
-a . |
(8.16) |
The first of these is obvious. The second follows from
Condition Eq. (8.16) follows from a similar reasoning.
We now solve Eqs. (8.13)-(8.16), obtaining
We shall not derive this here. One may check that Eq. (8.18)
indeed is the solution to Eq. (8.13) satisfying (8.14)-(8.16).
Now taking the limit
 we get
we get
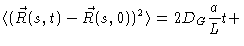 |
| |
|
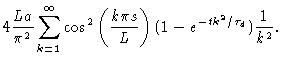 |
(8.20) |
For
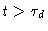 we get diffusive behaviour with diffusion constant
we get diffusive behaviour with diffusion constant
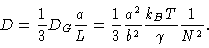 |
(8.21) |
Notice that this is proportional to N-2, whereas the diffusion
coefficient of the Rouse model was proportional to N-1. The reptation
result, N-2, is confirmed by experiments which measured the diffusion
coefficients of polymer melts as a function of their molecular weight.





Next: Viscoelastic behavior
Up: Dynamics of dense polymer
Previous: Mathematical definition of the
W.J. Briels
![\scalebox{0.5}{\includegraphics[36,402][550,722]{fig8_3.eps}}](img921.gif)
![\scalebox{0.5}{\includegraphics[36,402][550,722]{fig8_3.eps}}](img921.gif)
![]() is the Rouse time which is equal to
is the Rouse time which is equal to ![]() in chapter 6. The meaning
of
in chapter 6. The meaning
of ![]() and
and ![]() will become clear in the remaining part of
this section.
will become clear in the remaining part of
this section.
![]() .
.
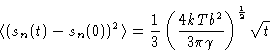
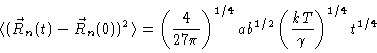
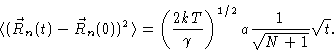
![]() it is useful to introduce
it is useful to introduce
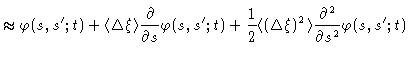
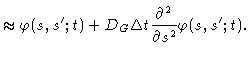
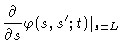
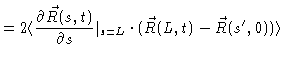
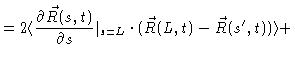
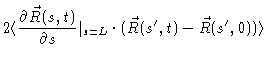
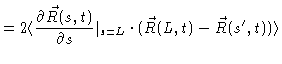
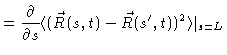
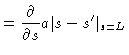
![]() we get
we get