Single elongated rigid particles in a shear flow trace out Jeffery orbits, named after the scientist who first described this motion. It is to be expected that in a dense system the particles will strongly interact and will not be able to perform Jeffery motion independently of each other. If there is any tumbling at all, this has to be performed by the particles collectively. In order to study this intriguing motion, we developed event-driven Brownian dynamics simulations [1,2].

collective tumbling

The picture on the left shows the start configuration of the simulation, with all rods oriented along the horizontal axis. For clarity, the ends of the rods are coloured red and green. A linear shear flow moves the top of the box to the right, and the bottom of the box to the left, as indicated by the yellow lines. Click here (29 MB) or on the picture to see what happens next. The actual simulated system contained 1750 rods, of which only 500 are shown in the movie. Each rod has an aspect ratio (L/D) of 25, the volume fraction of rods is 14%.

end-to-end vectors

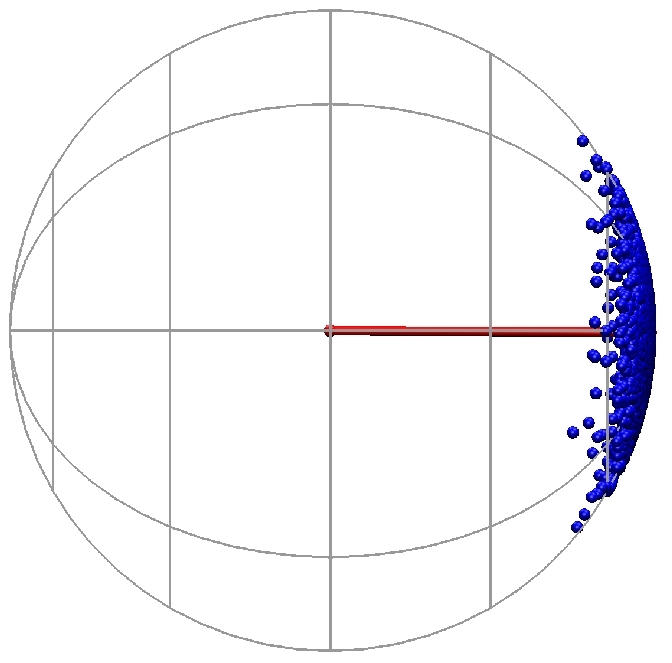
The blue dots in the picture on the right represent the end-to-end vectors of the rods, scattered over the surface of a sphere. Drawn in red is the director, i.e. the experimentally accessible average direction, which in this frame points along the flow direction. Click here (13 MB) or on the picture to watch the time evolution of the system. Since some rods are left behind during the tumbling, a diametrically opposed secondary cloud develops over several revolutions. This effect is also observable in the preceding movie.

director motion vs mesogen motion

Closer inspection of the simulations reveals that the rods and director do not tumble in the plane of the pictures but follow paths akin to that of paddles during kayaking. Our calculated tumbling periods for the director are in good agreement with recent experiments on sheared solutions of rod-like fd viruses. [1,3]. At high shear rates the director starts wagging up and down around the shear direction, accompanied by negative first and normal stress differences [4], and at even higher shear rates the director flow aligns along the shear direction, all in agreement with experiments. The simulations reveal, however, that the rods are always kayaking -- a reduced coherence at higher shear rates makes it impossible for the director to follow this motion faithfully [5].