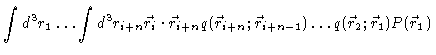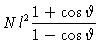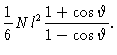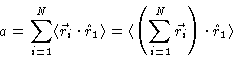Next: Appendix B
Up: The Gaussian chain
Previous: One Gaussian chain in
In the case of a freely rotating chain it is rather easy to calculate the mean square
end-to-end vector, the radius of gyration and the persistence length.
The freely rotating chain is defined by saying that the angles
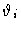 are fixed and that all
are fixed and that all 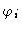 may randomly take a value in
may randomly take a value in ![$[0,2\pi]$](img324.gif) .
In order to treat this chain mathematically we introduce the probability
density in configuration space
.
In order to treat this chain mathematically we introduce the probability
density in configuration space
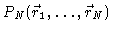 and define
and define
So
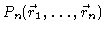 is the probability density to find the
first n bond vectors in the configuration
is the probability density to find the
first n bond vectors in the configuration
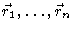 ,
and
,
and
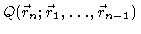 is the conditional
probability density to find bond vector n in state
is the conditional
probability density to find bond vector n in state 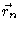 ,
given that
the preceding vectors are in configuration
,
given that
the preceding vectors are in configuration
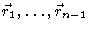 .
Integrating Eq. (3.35) over
.
Integrating Eq. (3.35) over 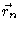 and using Eq. (3.34) we obtain
and using Eq. (3.34) we obtain
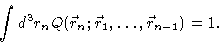 |
(3.36) |
In our case
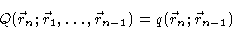 |
(3.37) |
i.e. the conditional probability to have vector n in state 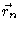 depends only on the state of vector n-1. In mathematics it is said that
the chain has the Markov property. Using the definitions given so far we may
write
depends only on the state of vector n-1. In mathematics it is said that
the chain has the Markov property. Using the definitions given so far we may
write
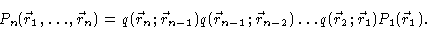 |
(3.38) |
We may now easily calculate all quantities of interest.
We first notice, that in the present case
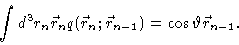 |
(3.39) |
Repeatedly using this equation we calculate
Using this in Eqs. (1.29) and (1.44) we get for large N :
Another quantity characteristic of the chain is the persistence length . It is defined by
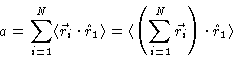 |
(3.43) |
and it gives the average of the projection of the end-to-end vector on the
direction of the first bond. For large N we may write Eq. (1.29
) like
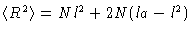 from which we get
from which we get
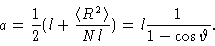 |
(3.44) |
We see that for a rod the persistence length is infinite.





Next: Appendix B
Up: The Gaussian chain
Previous: One Gaussian chain in
W.J. Briels
![]() are fixed and that all
are fixed and that all ![]() may randomly take a value in
may randomly take a value in ![]() .
In order to treat this chain mathematically we introduce the probability
density in configuration space
.
In order to treat this chain mathematically we introduce the probability
density in configuration space
![]() and define
and define