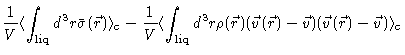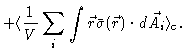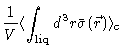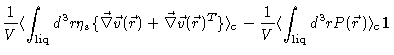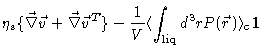Next: The Rouse chain
Up: The virial theorem, and
Previous: A. General
We now apply Eq. (5.61) to a volume containing solvent
molecules and solute particles . The sum over i then runs over solvent molecules and
solute particles. The averaging may be performed by a conditional average
given some particle configuration, followed by an average over all particle
configurations.
We first perform the sum over solvent molecules. Dividing the space occupied
by liquid into small cubes, large enough to be called a many body system,
but small enough for gradients of cube properties to be small, we may write
for the contribution of the solvent molecules
The averages are over particle configurations. The integrals in the first
two terms are over the space occupied by liquid. The sum in the last term is
over solute particles, and
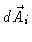 is a vectorial surface element of
particle i.
is a vectorial surface element of
particle i.
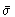 is the stress tensor in the solvent phase. The
last term is a contribution from the forces exerted by the solute particles
on the solvent.
is the stress tensor in the solvent phase. The
last term is a contribution from the forces exerted by the solute particles
on the solvent.
We now calculate the contribution from the solute particles. Averaging over
the solvent configurations turns
midvi/dt into
miDVi/Dtgiven in Eq. (4.39). The contribution to the stress tensor by
the solute particles then reads
where
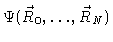 is the joint probability
function for the solute particles to be at positions
is the joint probability
function for the solute particles to be at positions
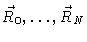 .
Combining the results we find
.
Combining the results we find
The sum of the second term in Eq. (5.62) and the first term in
Eq. (5.63) is equal to the total mass weighed velocity
fluctuation divided by the volume, and has been put equal to zero, which is
reasonable for macroscopic volumes of fluid.
The first term in Eq. (5.64) reads
In the second step we have used the fact that within the solute particle
velocity gradients are zero. In the third step we have used
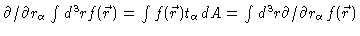 ,
for any function
,
for any function
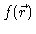 .
.





Next: The Rouse chain
Up: The virial theorem, and
Previous: A. General
W.J. Briels