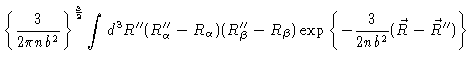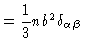Next: Stochastic processes
Up: The Gaussian chain
Previous: Appendix B
We shall first show that for small n we may write
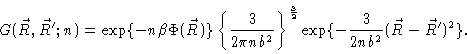 |
(3.50) |
Taking the limit for
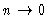 we then easily check Eq. (3.16). In order to prove Eq. (3.50) we first
notice that n being small, all Ri in the exponent in Eq. (3.13) are approximately equal to
we then easily check Eq. (3.16). In order to prove Eq. (3.50) we first
notice that n being small, all Ri in the exponent in Eq. (3.13) are approximately equal to 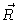 ,
from which it
follows that
,
from which it
follows that
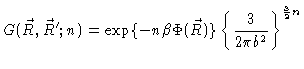 |
| |
|
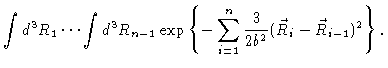 |
(3.51) |
It is now simply a matter of successively performing the integrals. The
simplest way to do this is by induction.
The first equals sign is the induction step, and the second one is the final
proof.
Now look at the Chapman-Kolmogorov equation (3.14), and take n to
be small. Then
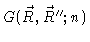 differs from zero only if
differs from zero only if
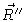 is in the neighbourhood of
is in the neighbourhood of 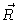 .
We therefore
expand the second factor
.
We therefore
expand the second factor
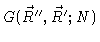 in Eq. (3.14) with respect to
in Eq. (3.14) with respect to
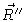 .
.
where
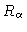 denotes the
denotes the 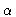 'th Cartesian component of
'th Cartesian component of 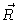 .
Introducing Eqs. (3.50) and (3.53) into (
3.14) we get
.
Introducing Eqs. (3.50) and (3.53) into (
3.14) we get
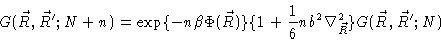 |
(3.54) |
where we have used
| |
|
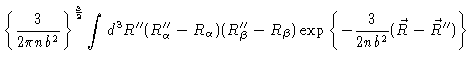 |
|
| |
|
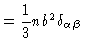 |
(3.55) |
For small n, we expand the exponent
 |
(3.56) |
Collecting terms of order n, and using
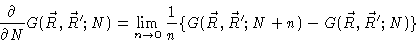 |
(3.57) |
we finally arrive at Eq. (3.15).





Next: Stochastic processes
Up: The Gaussian chain
Previous: Appendix B
W.J. Briels
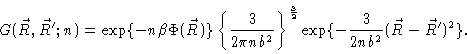
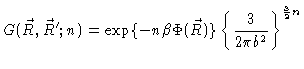
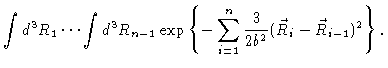
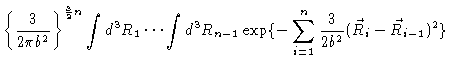
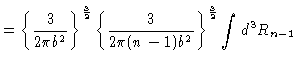
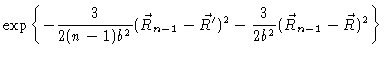
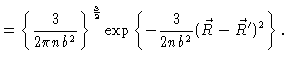
![]() differs from zero only if
differs from zero only if
![]() is in the neighbourhood of
is in the neighbourhood of ![]() .
We therefore
expand the second factor
.
We therefore
expand the second factor
![]() in Eq. (3.14) with respect to
in Eq. (3.14) with respect to
![]() .
.