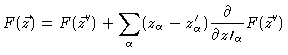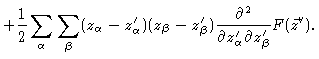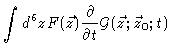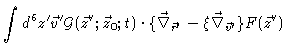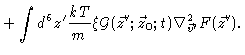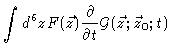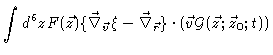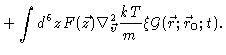Next: Appendix B
Up: Stochastic processes
Previous: The Smoluchowski equation
We shall derive the Fokker-Planck equation by looking at
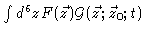 for any function
for any function
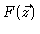 .
Because we are always interested in averages like this, equations that may
be derived using this object are all we need. (In mathematical terms
.
Because we are always interested in averages like this, equations that may
be derived using this object are all we need. (In mathematical terms
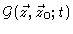 is a distribution or generalized
function, not an ordinary function).
is a distribution or generalized
function, not an ordinary function).
Our proof very much resembles the one in Appendix 3.C. Our starting point is
again the Chapman-Kolmogorov equation
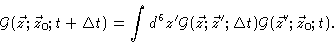 |
(4.40) |
Multiplying by
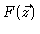 and integrating yields
and integrating yields
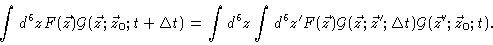 |
(4.41) |
Now we shall perform the integral with respect to z on the right hand
side. Because
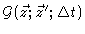 differs
from zero only when
differs
from zero only when  is in the neighbourhood of
is in the neighbourhood of
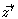 ,
we expand
,
we expand
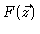 around
around
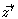
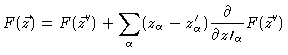 |
| |
|
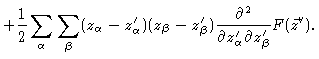 |
(4.42) |
Introducing this into Eq. (4.41) we get
Now we make use of
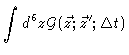 |
= |
1 |
(4.44) |
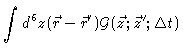 |
= |
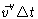 |
(4.45) |
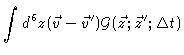 |
= |
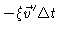 |
(4.46) |
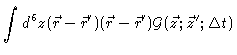 |
= |
0 |
(4.47) |
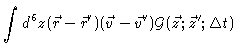 |
= |
0 |
(4.48) |
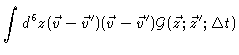 |
= |
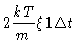 |
(4.49) |
which hold true to the first order in 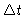 .
The first three of these
equations are obvious. The last three easily follow from the Langevin
equation in section 4.1 together with the
fluctuation-dissipation theorem Eq. (4.21). 1
in Eq. (4.49) denotes the 3-dimensional unit matrix.
Introducing everything into Eq. (4.43), dividing by
.
The first three of these
equations are obvious. The last three easily follow from the Langevin
equation in section 4.1 together with the
fluctuation-dissipation theorem Eq. (4.21). 1
in Eq. (4.49) denotes the 3-dimensional unit matrix.
Introducing everything into Eq. (4.43), dividing by 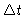 and taking the limit
and taking the limit
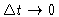 ,
we get
,
we get
Next we change the integration variable
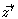 into
into  and perform some partial integrations, obtaining
and perform some partial integrations, obtaining
Because this has to hold true for all possible
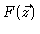 we conclude
that the Fokker-Planck equation (4.14) must hold true.
we conclude
that the Fokker-Planck equation (4.14) must hold true.





Next: Appendix B
Up: Stochastic processes
Previous: The Smoluchowski equation
W.J. Briels
![]() for any function
for any function
![]() .
Because we are always interested in averages like this, equations that may
be derived using this object are all we need. (In mathematical terms
.
Because we are always interested in averages like this, equations that may
be derived using this object are all we need. (In mathematical terms
![]() is a distribution or generalized
function, not an ordinary function).
is a distribution or generalized
function, not an ordinary function).