The Rouse chain

We now concentrate on one bead, say bead no. n, while keeping all the other beads fixed. Its equilibrium distribution is given by

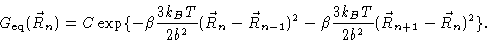$$G_{\mathrm{eq}}( \vec{R}_{n})=C\exp \{-\beta \frac{3k_{B}T}{2... ...\beta \frac{3k_{B}T}{2b^{2}}(\vec{R}_{n+1}-\vec{R}_{n})^{2}\}.$$ (6.1)

According to Eq. (4.30) and Eq. (4.27) the Langevin equation  describing the motion of the bead then is, with $\gamma =m\xi$

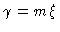
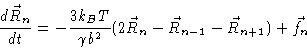$$\frac{d\vec{R}_{n}}{dt}=-\frac{3k_{B}T}{\gamma b^{2}}(2\vec{R}_{n}-\vec{R} _{n-1}-\vec{R}_{n+1})+\vec{f}_{n}$$ (6.2)

where we have assumed that 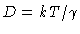$D=kT/\gamma$ is independent on 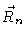$\vec{R}_{n}$. The same reasoning may be applied to all other beads, leaving us with the equations of motion

    

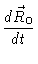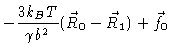$$\frac{d\vec{R}_{0}}{dt} -\frac{3k_{B}T}{\gamma b^{2}}(\vec{R}_{0}-\vec{R} _{1})+\vec{f}_{0}$$ = (6.3)

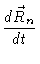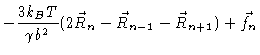$$\frac{d\vec{R}_{n}}{dt} -\frac{3k_{B}T}{\gamma b^{2}}(2\vec{R}_{n}-\vec{R} _{n-1}-\vec{R}_{n+1})+\vec{f}_{n}$$ = (6.4)

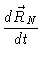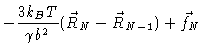$$\frac{d\vec{R}_{N}}{dt} -\frac{3k_{B}T}{\gamma b^{2}}(\vec{R}_{N}-\vec{R} _{N-1})+\vec{f}_{N}$$ = (6.5)

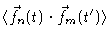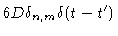$$\langle \vec{f}_{n}(t)\cdot \vec{f}_{m}(t^{\prime })\rangle 6D\delta _{n,m}\delta (t-t^{\prime })$$ = (6.6)

Eq. (6.4) applies when $n=1,\ldots ,N-1$.

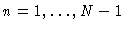Before starting to analyse these equations in the next section, let us derive one simple result:

$$\frac{d \vec{R}_G}{dt} \frac{1}{N+1} \sum_{n=0}^N \vec{f}_n$$ = (6.7)

$$\vec{R}_G(t) \vec{R}_G(0) + \int_0^t d\tau \frac{1}{N+1} \sum_n \vec{f}_n(\tau)$$ = (6.8)

 

$$\langle (\vec{R}_G(t) - \vec{R}_G(0))^2 \rangle \langle \int_0^t d\tau \int_0^t d\tau ^{\prime}\left( \frac{1}{N+... ...ht) \cdot \left( \frac{1}{N+1} \sum_m \vec{f}_m (\tau^{\prime}) \right) \rangle$$ =

$$\frac{6D}{N+1}t = 6D_G t$$ = (6.9)

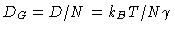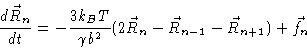
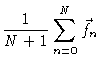
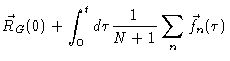
So $D_G = D/N = k_BT /N\gamma$, which is perfectly understandable.