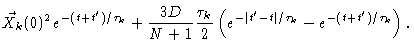Next: Monomer motion
Up: The Rouse chain
Previous: Normal mode analysis
As an example of a dynamic characteristic of the Rouse chain we calculate
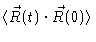 ,
i.e. the time correlation
function of the end-to-end vector . First we notice that
,
i.e. the time correlation
function of the end-to-end vector . First we notice that
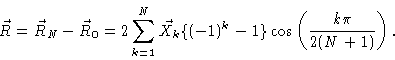 |
(6.35) |
Our result will be dominated by k values which are extremely small
compared to N. We therefore write
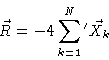 |
(6.36) |
where the prime at the summation sign indicates that only terms with odd kshould occur in the sum. Then
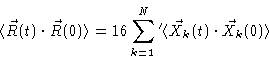 |
(6.37) |
where we have used the fact that different modes are uncorrelated.
From Eqs. (6.32) to (6.33) we get
In Appendix A of this chapter it is shown that
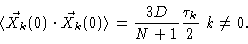 |
(6.40) |
Introducing everything into Eq. (6.37) we get
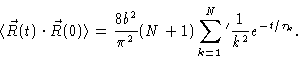 |
(6.41) |
The characteristic decay time at large t is 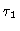 ,
which is
proportional to N2.
,
which is
proportional to N2.
Notice that in this derivation we have averaged over all initial values. We
might also have calculated
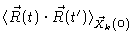 ,
i.e. the time correlation function of
,
i.e. the time correlation function of
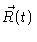 ,
given some initial configurations of the chain. For very large t and
,
given some initial configurations of the chain. For very large t and
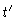 the result should be independent of
the result should be independent of
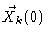 .
Indeed using
Eq. (6.38) twice, it is not difficult to find
.
Indeed using
Eq. (6.38) twice, it is not difficult to find
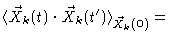 |
| |
|
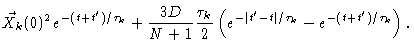 |
(6.42) |
which for very large t and
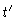 leads to the desired result.
leads to the desired result.





Next: Monomer motion
Up: The Rouse chain
Previous: Normal mode analysis
W.J. Briels
![]() ,
i.e. the time correlation
function of the end-to-end vector . First we notice that
,
i.e. the time correlation
function of the end-to-end vector . First we notice that
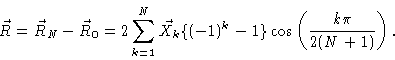
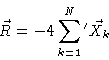
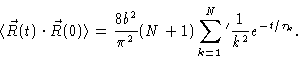
![]() ,
i.e. the time correlation function of
,
i.e. the time correlation function of
![]() ,
given some initial configurations of the chain. For very large t and
,
given some initial configurations of the chain. For very large t and
![]() the result should be independent of
the result should be independent of
![]() .
Indeed using
Eq. (6.38) twice, it is not difficult to find
.
Indeed using
Eq. (6.38) twice, it is not difficult to find