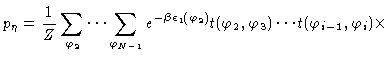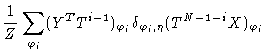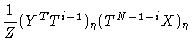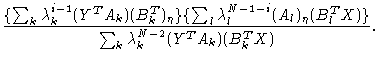Next: The mean square end-to-end
Up: The Rotational Isomeric State
Previous: The partition function
It is instructive to calculate some probabilities occurring in the RIS
model. An important probability for computer simulations is the conditional
probability
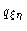 defined below. We shall always assume that
the chain is infinitely long, and that end effects may be neglected. In this
case
defined below. We shall always assume that
the chain is infinitely long, and that end effects may be neglected. In this
case
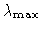 is the only eigenvalue we need.
is the only eigenvalue we need.
We define the probability that a given bond is in state 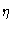 by
by
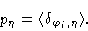 |
(1.19) |
Explicitly introducing the averaging procedure yields
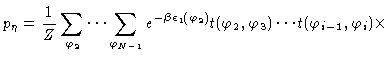 |
| |
|
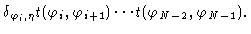 |
(1.20) |
Using the same method as in the previous section we find
Dividing numerator and denominator by
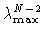 ,
and
assuming N, i, and N-i are large we get
,
and
assuming N, i, and N-i are large we get
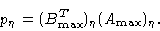 |
(1.22) |
Because here and in the remaining part of the chapter we only need
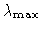 and the corresponding vectors
Amax and
B
maxT, we shall omit the subscript ''max'' and write
and the corresponding vectors
Amax and
B
maxT, we shall omit the subscript ''max'' and write
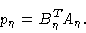 |
(1.23) |
Similarly one calculates
An important quantity is
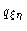 ,
the conditional probability to find
bond i in state
,
the conditional probability to find
bond i in state 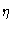 ,
given that bond i-1 is in state
,
given that bond i-1 is in state 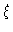
 |
(1.25) |
Introducing Eqs. (1.23) and (1.24) we get
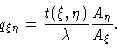 |
(1.26) |
This quantity may be used to generate chain conformations on a computer.





Next: The mean square end-to-end
Up: The Rotational Isomeric State
Previous: The partition function
W.J. Briels
![]() defined below. We shall always assume that
the chain is infinitely long, and that end effects may be neglected. In this
case
defined below. We shall always assume that
the chain is infinitely long, and that end effects may be neglected. In this
case
![]() is the only eigenvalue we need.
is the only eigenvalue we need.
![]() by
by