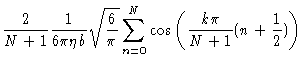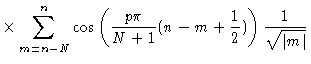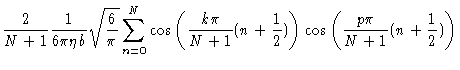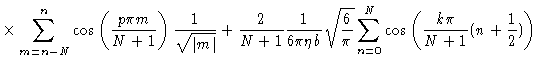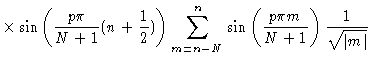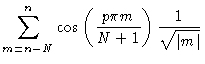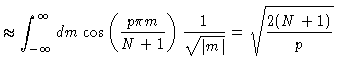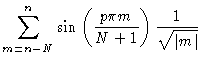



Next: Dynamics of dense polymer
Up: The Zimm chain
Previous: Diffusion coefficient and viscosity
In order to derive Eq. (7.15) we write
We now approximate
Introducing these results into Eq. (7.30) one finds Eq. (7.15). As a technical detail we notice that in principle diagonal
terms in Eq. (7.14) should have been treated separately, which
is clear from Eq. (5.56). Since the contributions of all other
terms is proportional to N1/2, we omit the diagonal terms.

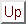



Next: Dynamics of dense polymer
Up: The Zimm chain
Previous: Diffusion coefficient and viscosity
W.J. Briels