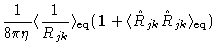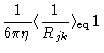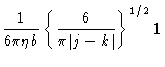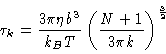Next: Diffusion coefficient and viscosity
Up: The Zimm chain
Previous: Definition and equations of
If we introduce the mobility tensors Eq. (5.56) into Eq. (7.7),
we are left with a completely intractable set of equations. One way out of
this is by noting that in equilibrium, on average, the mobility tensors will
be proportional to the unit tensor. We therefore assume that 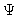 will
never differ much from
will
never differ much from
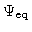 ,
and that we may replace the
mobility tensor in Eq. (7.7) by
,
and that we may replace the
mobility tensor in Eq. (7.7) by
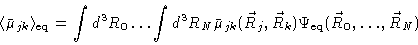 |
(7.10) |
where
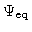 is the Gaussian equilibrium distribution. A
simple calculation yields
is the Gaussian equilibrium distribution. A
simple calculation yields
The next step is to write down the equations of motion of the normal
coordinates Eq. (6.26):
where
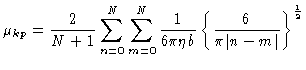 |
| |
|
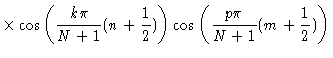 |
(7.14) |
Equation (7.12) still is not tractable. It turns out however
(see Appendix), that for large N approximately
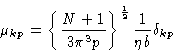 |
(7.15) |
Introducing this result in Eq. (7.12), we see that the normal
modes , just like with the Rouse chain, constitute a set of
decoupled coordinates.
For small values of k we find
where the first term on the right hand side of Eq. (7.16) equals
zero when k=0, and otherwise
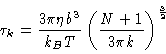 |
(7.18) |
We are now in a position to calculate the diffusion coefficient DG of a
Zimm chain, and the viscosity of a dilute solution of Zimm chains.





Next: Diffusion coefficient and viscosity
Up: The Zimm chain
Previous: Definition and equations of
W.J. Briels
![]() will
never differ much from
will
never differ much from
![]() ,
and that we may replace the
mobility tensor in Eq. (7.7) by
,
and that we may replace the
mobility tensor in Eq. (7.7) by